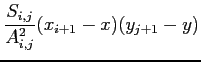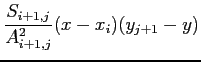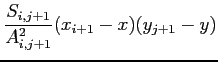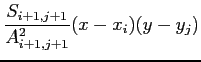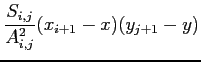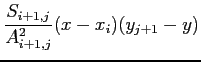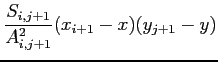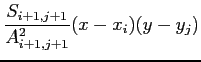Next: The Stationary Poisson Equation
Up: Coupling between Monte Carlo
Previous: Introduction
Contents
Since the number of particles in a simulation is quite limited, if compared to the number of particles in a real semiconductor device, noise will always be present in the solutions generated by GNU Archimedes. That is why we have to use an advanced algorithm in order to avoid, as the best as possible, this noise, instead of simply counting the number of particles in the cells of the simulation. For this purpose, we use in GNU Archimedes the well-known cloud-in-cell algorithm. For more informations about cloud-in-cell method and more advanced algorithms see the following papers
- S.E.Laux, "On Particle-Mesh Coupling in Monte Carlo Semiconductor Device Simulation", IBM Research Report, RC 20101
- S.E.Laux, "On Particle-Mesh Coupling in Monte Carlo Semiconductor Device Simulation", IBM Research Report, RC 20081
We report here a brief description of the cloud-in-cell method.
Let us consider a finite difference mesh with the nodes located at 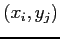 . Let us denote by
. Let us denote by 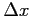 and
and 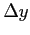 the constant spatial step in the
the constant spatial step in the 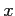 -direction and
-direction and 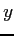 -direction. Then, if we denote by
-direction. Then, if we denote by 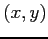 the point coordinates in which one wants to compute the density charge, with
the point coordinates in which one wants to compute the density charge, with
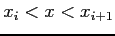 and
and
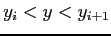 , we compute the density in the following way
, we compute the density in the following way
where 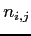 is the density located at
is the density located at 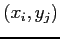 ,
, 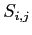 the statistical weight of the particles located at
the statistical weight of the particles located at 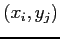 and
and
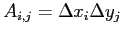 .
Methods do exist that avoid the problems of self-forces but they are necessary only when the grid is not regular and when we deal with heterostructures. They are not implemented, at the present time, in GNU Archimedes because do not yet deal with such structures. They will be implemented in the next future.
.
Methods do exist that avoid the problems of self-forces but they are necessary only when the grid is not regular and when we deal with heterostructures. They are not implemented, at the present time, in GNU Archimedes because do not yet deal with such structures. They will be implemented in the next future.




Next: The Stationary Poisson Equation
Up: Coupling between Monte Carlo
Previous: Introduction
Contents
Didier Link
2007-05-18