13.1 Example 1

The curve of a road section has a steepness of 18 degrees and a curvature radius of 230 meters. If the coefficient of static friction between the tires of a car and the road is 0.33, find: a) The maximum speed at which the car can make the turn, b) The speed for which there is no friction force between the tires and the road and, c) The minimum speed at which the car can make the turn.

Solution with FisicaLab

Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add one element Stationary reference system, one element Mobile with perpendicular circular movement, one element Force and one element Friction. As show the image below:

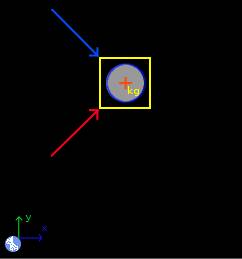
The element Stationary reference system write to default the gravity value. And the time is irrelevant for this problem. Now to the element Mobile with perpendicular circular movement, that represent the car, and since the car’s mass is not provided (it is irrelevant for the requested data), we write 1 kg, and we add the conversion factor km/h to the velocity. Also we write as unknown the tangential force, even when tangential acceleration is 0, to satisfy the requirement of number of unknowns. And we let the center of rotation placed to the right, that corresponds with the applied forces:

Name

0

m

1

vt

vt @ km/h

r

230

at

0

Ft

Ft

C

>

For the element Force, which represents the normal, and taking into account that the steepness of the curve is 18 degrees, we have:

f

normal

ang

72

And to the friction force:

N

normal

u

0.33

ang

18

Now click in the icon Solve to get the answer:

normal = 11.554 N ;  vt = 146.462 km/h ;  Ft = 0.000 N ;
Status = success.

For part b, first remove the friction element, since there should be no friction force:

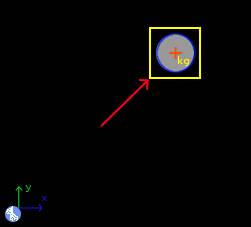
And click in the icon Solve to get the answer:

normal = 10.315 N ;  vt = 97.474 km/h ;  Ft = 0.000 N ;
Status = success.

Now to part c, add again a friction force:

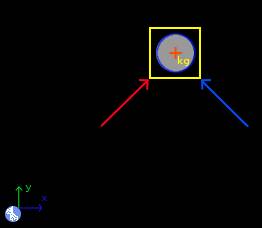
With data:

N

normal

u

0.33

ang

18

And click again in the icon Solve to get the answer:

normal = 9.316 N ;  vt = 0.503 km/h ;  Ft = 0.000 N ;
Status = the iteration has not converged yet.

What does this mean? That there is no minimum speed. The given coefficient of friction is enough for park the car on the curve without slipping.