GNU FísicaLab: Example 10 (cd)

13.10 Example 10

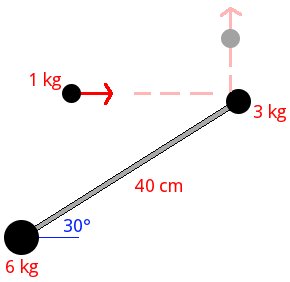
Three masses are on an horizontal frictionless surface. Two of these, 3 and 6 kg, are at rest and are linked by a lightweight rod. The third, of 1 kg, moves with a speed of 4 m/s as shown in the image. If this collide with mass of 3 kg and bounces at 90 degrees with a speed of 2 m/s. What will be the subsequent movement of the other two masses? Also obtain the absolute velocity of the masses of 3 and 6 kg just after impact.

Solution with FisicaLab

Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add two elements Mobile with linear movement, two elements Mobile with circular movement, one element Center of rotation, one element Final system, two elements Angular velocity, two elements Absolute velocity, one element Angular momentum and one element Linear momentum. As show the image below:

The element Mobile with linear movement to the left represents the mass of 1 kg in the initial state. Assuming the mass of 6 kg is at the origin of the coordinate system, we have for this element, called initial:

Name: initial
m: 1
v: 4
x: 0
y: 20 @ cm
ang: 0
a: 0

To the other Mobile with linear movement, which represents the same mass of 1 kg but in the final state, we have, calling it A (the X coordinate is 40*cos(30), this can be operated directly at text field):

Name: A
m: 1
v: 2
x: 34.641 @ cm
y: 0
ang: 90
a: 0

To the element Center of rotation, around which the masses of 3 and 6 kg rotate in the final state, we first find its coordinates. Noting that the distance from the mass of 6 kg is 13,333 m, we have (these operations can be done directly at text fields):

x = 13.333*cos(30) = 11.547
y = 13.333*sin(30) = 6.666

Thus we have for this element:

Name: center
v: vCenter
ang: angCenter
x: 11.547 @ cm
y: 6.666 @ cm

Now for the element Mobile with circular movement to the right, that represents the mass of 3 kg in the final state, we have, calling it B (the distance from the center can be calculated with the function rd()):

Name: B
m: 3
vt: vtB
r: 26.666 @ cm
y: 0

To the other element Mobile with circular movement, that represents the mass of 6 kg in the final state, we have, calling it C (the distance from the center can be calculated with the function rd()):

Name: C
m: 6
vt: vtC
r: 13.333 @ cm
y: 0

These two elements have the same angular velocity. Therefore for the Angular velocity elements, respectively:

Object: B
vang: vang

Object: C
vang: vang

These three mobiles and the center of rotation constitute the final state, then we add them to the element Final system, that we call final:

Name: final
Object 1: center
Object 2: A
Object 3: B
Object 4: C

Since are requested the absolute velocity of masses 3 and 6 kg (B and C), we have for the elements Absolute velocity, respectively:

Object: B
angR: 30
Center: center
v: vB
ang: angB

Object: C
angR: 210
Center: center
v: vC
ang: angC

To the element Angular momentum, taking into account that no external moments applied:

System i: initial
System f: final
M: 0

And to element Linear momentum, no external forces are applied, we have:

System i: initial
System f: final
Fx: 0
Fy: 0

Now click in the icon Solve to get the answer:

vang = -3.110 rad/s ;  vtC = -0.415 m/s ;
vB = 1.274 m/s ;  angB = 312.412 degrees ;
vtB = -0.829 m/s ;  vC = 0.274 m/s ;
angC = 30.004 degrees ;  vCenter = 0.497 m/s ;
angCenter = 333.435 degrees ;
Status = success.

Note: Note that in this problem the masses of 3 and 6 kg does not appear in the initial state. This is because for these problems FisicaLab allows only one object in the initial state. The object that initially is moving. See previous example.