GNU FísicaLab: Example 10 (rs)

9.10 Example 10

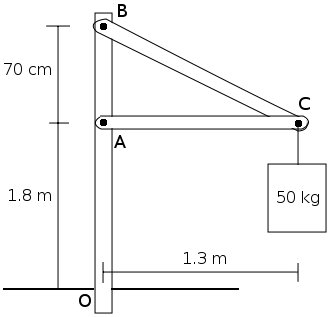
Consider the structure in the image below. Calculate reactions at O and reactions between the beams at points A, B and C. Ignore the weight of the beams.

Solution with FisicaLab

Select the group Static and, inside this, the module Static of solids. Erase the content of the chalkboard and select the SI system. And add one element Stationary reference system, three elements Beam, seven elements of beam and the necessary elements Force and Couple, as show the image below (the yellow lines separate the areas where are defined the beams):

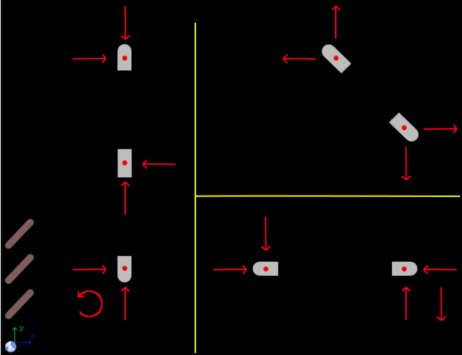
In the image can be seen that, according to Newton’s third law, the reactions between the beams have a different sense. And we assign the same magnitude or unknown data. The Stationary reference system set the gravity value to default. Now to the element Beam that represent the vertical beam, that we call OAB:

Name: OAB
m: 0
lc: 0
ang: 90

This beam is composed of three elements, which represent the points O, A and B. For the element in O, and their respective reactions, called Rx, Ry, M, we have:

Name: OAB
l: 0

f: Rx

f: Ry

M: M

For the element in A and their respective reactions, RAx and RAy, we have:

Name: OAB
l: 1.8

f: RAx

f: RAy

For the element in B and their respective reactions, RBx and RBy, we have:

Name: OAB
l: 2.5

f: RBx

f: RBy

Now for the element Beam representing the horizontal beam, that we call AC, we have:

Name: AC
m: 0
lc: 0
ang: 0

For the element of beam that represent the point A, and to its respective reactions, we have:

Name: AC
l: 0

f: RAx

f: RAy

To the element of beam at point C, for the reactions RCx, RCy and to the weight of 50 kg (50 kg*9.81 m/s2 = 490.5 N), we have:

Name: AC
l: 1.3

f: RCx

f: RCy

f: 490.500

Now to the element Beam that represent the beam from B to C, that we call BC (here the angle is entered as slope -0.7/1.3):

Name: BC
m: 0
lc: 0
ang: -28.301

To the element of beam at B and to its reactions, we have:

Name: BC
l: 0

f: RBx

f: RBy

For the element of beam at C, we should calculate the distance between B and C. Which can be calculated with hypot(0.7,1.3):

Name: BC
l: 1.476

And to the reactions RCx and RCy (we don’t add here the weight of the 50 kg, because was added at the beam AC):

f: RCx

f: RCy

Now click in the icon Solve to get the answer:

RAx = 910.919 N ;  RAy = -0.000 N ;  RCy = 490.500 N ;
RCx = 910.919 N ;  RBx = 910.919 N ;  RBy = 490.500 N ;
M = 637.643 N*m ;  Ry = 490.500 N ;  Rx = 0.000 N ;
Status = success.

Note: A more easy way to solve this problem (that avoid having to calculating the length of the beam BC), is replace the BC beam with two elements Beam of 2 forces (notice that the beam BC is an element that supports two forces). See image below. Everything is a matter of deciding which is best for the problem to solve. The beam AC is also a beam of two forces. However, we can’t replace both.