9.13 Example 13

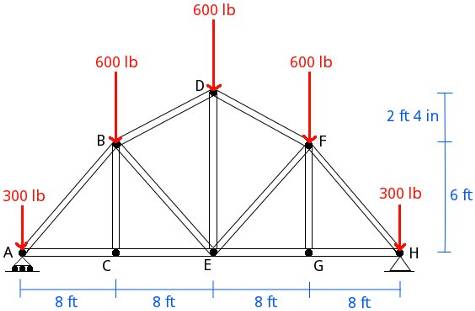
In the truss of the image, find the support reactions and internal forces in all beams under the load conditions shown.

Solution with FisicaLab

Select the group Static and, inside this, the module Static of solids. Erase the content of the chalkboard and select the English system. Then add one element Truss, eight elements Joint of truss, eight elements Force, five forces for the load forces and three for the support reactions (notice that in support A there is only one vertical force), and 26 elements Beam of truss to build the problem as show below:

To the element Truss, we use the name AH:

Name

AH

All the elements Joint of truss, will owned by this truss. So, we add each joint to this truss:

Truss

AH

For the two elements Beam of truss that represent the beam from joint A to C, and calling AC the internal force, we have:

t

AC

Now for the two elements Beam of truss that represent the beam from joint A to B, and calling AB the internal force and entering the angle as the slope 6/8, we have:

t

AB

ang

36.870

For the two elements Beam of truss that represent the beam from joint B to C, and calling BC the internal force, we have:

t

BC

For the two elements Beam of truss that represent the beam from joint B to E, and calling BE the internal force, we have:

t

BD

ang

16.260

Here the angle is entered as slope 28/96. The numerator and denominator should be at the same units: 2 ft 4 in = 28 in and 6 ft = 96 in. Also can be used 2.333/6 using the feet unit. Now for the two elements Beam of truss that represent the beam from joint B to E, and calling BE the internal force, we have:

t

BE

ang

36.870

Here the angle is also the slope 6/8. For the two elements Beam of truss that represent the beam from joint C to E, and calling CE the internal force, we have:

t

CE

For the two elements Beam of truss that represent the beam from joint D to E, and calling DE the internal force, we have:

t

DE

Now for the two elements Beam of truss that represent the beam from joint D to F, and calling DF the internal force, we have:

t

DF

ang

16.260

Here the angle is entered as slope 28/96. For the two elements Beam of truss that represent the beam from joint E to F, and calling EF the internal force, we have:

t

EF

ang

36.870

Here the angle is entered as slope 6/8. Now for the two elements Beam of truss that represent the beam from joint E to G, and calling EG the internal force, we have:

t

EG

For the two elements Beam of truss that represent the beam from joint F to G, and calling FG the internal force, we have:

t

FG

For the two elements Beam of truss that represent the beam from joint F to H, and calling FH the internal force, we have:

t

FH

ang

36.870

Here the angle is entered as slope 6/8. Now for the two elements Beam of truss that represent the beam from joint G to H, and calling GH the internal force, we have:

t

GH

Now to the element Force that represent the reaction in A:

f

RAy

And to the two elements Force that represent the reactions in H:

f

RHy

f

RHx

Now to the elements Force that represent the load forces, three of 600 lb and two of 300 lb:

f

300

f

600

Now click in the icon Solve to get the answer:

FG = 0.000 lb [tension] ;  EF = -59.993 lb [compression] ;
DF = -1200.000 lb [compression] ;  RAy = 1200.000 lb ;
FH = -1499.996 lb [compression] ;
AC = 1199.996 lb [tension] ;
AB = -1499.996 lb [compression] ;
GH = 1199.996 lb [tension] ;
RHy = 1200.000 lb ;  RHx = 0.000 lb ;
BC = -0.000 lb [compression] ;
CE = 1199.996 lb [tension] ;
BD = -1200.000 lb [compression] ;
DE = 71.992 lb [tension] ;  BE = -59.993 lb [compression] ;
EG = 1199.996 lb [tension] ;
Status = success.