13.4 Example 4

A 1.5 kg collar can slide without friction along a horizontal bar and is attached to two springs of constant 380 N/m, whose undeformed length is 2 cm. If the collar is released from rest in position A, find its speed when passing through point B.

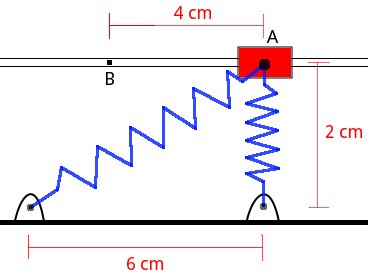
Solution with FisicaLab

Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add one element Stationary reference system, one element Object in rest, one element Mobile with linear movement, four elements Spring, seven elements Force, one element Initial system, one element Final system and one element Energy. As show the image below:

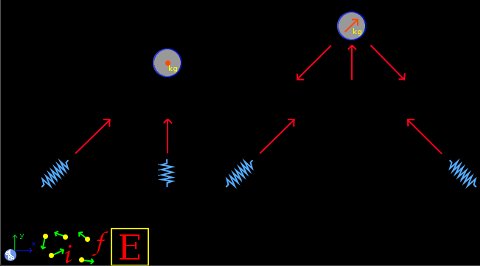
The element Stationary reference system write to default the gravity value. And the time is irrelevant for this problem. To the element Object in rest, which represents the collar in A, we have:

Name

initialCollar

m

1.5

y

0

To the Spring element in the vertical position, we have (this spring is neither stretched nor compressed):

Name

springOne

k

380

x

0

Now for the force applied to the spring:

f

forceOne

And to the second spring at the initial state, previously we get the stretched distance, we have (this operation can be done with hypot(6,2)-2  cm):

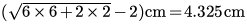
Name

springTwo

k

380

x

4.325 @ cm

And to the applied force (here the angle is irrelevant):

f

forceTwo

ang

0

The element Object in rest and the two springs, are the initial state. Then we add them to the Initial system element, that we call initial:

Name

initial

Object 1

initialCollar

Object 2

springOne

Object 3

springTwo

Object 4

0

For the element Mobile with linear movement, which represents the collar at point B, and since the movement is horizontal (angle = 0) and the acceleration is unknown, we have (the coordinates x,y are irrelevant to this problem):

Name

finalCollar

m

1.5

v

v

x

0

y

0

ang

0

a

acceleration

For the vertical force, which represents the normal applied by the horizontal bar, we have:

f

normal

Now, to the force applied at left, the force applied by the spring to the left, and entering the angle as 2/2, we have:

f

forceThree

ang

45.000

And to the force applied at right, the force applied by the spring to the right, and entering the angle as 2/4, we have:

f

forceFour

ang

26.565

Now to the Spring element at left, previously we get the stretched distance (this operation can be done with hypot(2,2)-2  cm):

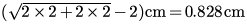
Name

springThree

k

380

x

0.828 @ cm

And to the applied force (here the angle is irrelevant):

f

forceThree

ang

0

Now to the Spring element at right we have, previously we get the stretched distance (this operation can be done with hypot(4,2)-2  cm):

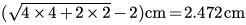
Name

springFour

k

380

x

2.472 @ cm

And to the applied force (here the angle is irrelevant):

f

forceFour

ang

0

The element Mobile with linear movement and the two previous springs, are the final state. Then we add them to the Final system element, that we call final:

Name

final

Object 1

finalCollar

Object 2

springThree

Object 3

springFour

Object 4

0

Finally, add the elements initial and final system in the element Energy. And knowing that energy is conserved, we have:

System i

initial

System f

final

W

0

Now click in the icon Solve to get the answer:

normal = 21.141 N ;  forceThree = 3.146 N ;
forceFour = 9.394 N ;  forceTwo = 16.435 N ;
forceOne = -0.000 N ;  v = 0.549 m/s ;
acceleration = 4.118 m/s2 ;
Status = success.

The collar speed is 0,549 m/s.