13.5 Example 5

A collar of 430 grams can slide without friction along a horizontal rod, which in turn can rotate about a vertical axis. A spring of constant 4 N/m, whose undeformed length is 70 cm, holds the collar to the bar, as shown in the figure below. Initially the bar is turning with a constant angular velocity of 13 rad/s. While a rope holds the collar in the position A. Suddenly the rope breaks and the spring pushes the collar out. Neglecting the mass of the rod, find the tangential velocity of the collar to the position B and its radial acceleration.

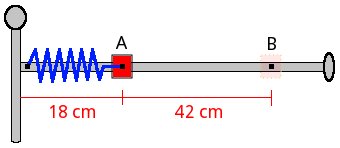
Solution with FisicaLab

Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add one element Stationary reference system, one element Mobile with circular movement, one element Mobile with polar circular movement, two elements Spring, three elements Force, one element Initial system, one element Final system, one element Energy, one element Angular momentum and one element Angular velocity. As show the image below:

The element Stationary reference system write to default the gravity value. And the time is irrelevant for this problem. Now to the element Mobile with circular movement, which represents the collar in A and taking in account that tangential velocity is unknown, we have:

Name

initialCollar

m

430 @ g

vt

vInitial

r

18 @ cm

y

0

And in the element Angular velocity we set the provided angular velocity for initial state:

Object

initialCollar

vang

13

For the Spring element of the initial state:

Name

initialSpring

k

4

x

-52 @ cm

And to the applied force:

f

initialForce

Now add this element Spring and the element Mobile with circular movement, which represents the initial state, to the element Initial system, that we call initial:

Name

initial

Object 1

initialCollar

Object 2

initialSpring

Object 3

0

Object 4

0

Now to the element Mobile with polar circular movement, which represents the collar in position B, we have:

Name

finalCollar

m

430 @ g

vt

vtFinal

r

60 @ cm

y

0

vr

vrFinal

ar

arFinal

And to the applied force to this element, the force applied by the spring, we have:

f

finalForce

This force is necessary to find the radial acceleration. Now to the element Spring of final state:

Name

finalSpring

k

4

x

-10 @ cm

And to the applied force:

f

finalForce

Now add this element Spring and the element Mobile with polar circular movement, which represents the final state, to the element Final system, that we call final:

Name

final

Object 1

finalCollar

Object 2

finalSpring

Object 3

0

Object 4

0

And add the elements initial and final system in the element Energy. And knowing that energy is conserved, we have:

System i

initial

System f

final

W

0

And in the element Angular momentum, we add the elements that represents the initial and final collar:

System i

initialCollar

System f

finalCollar

M

0

Now click in the icon Solve to get the answer:

initialForce = 2.080 N ;  finalForce = 0.400 N ;
vInitial = 2.340 m/s ;  vtFinal = 0.702 m/s ;
vrFinal = 2.721 m/s ;  arFinal = 0.930 m/s2 ;
Status = success.