13.7 Example 7

Two small spheres of 300 grams can slide without friction along a horizontal thin bar, which in turn can rotate about a vertical axis. Initially the bar is rotating at a constant angular speed of 9 rad/s, while a rope holds both spheres at a distance of 15 cm from the axis of rotation. Suddenly the rope breaks and the spheres stops at the ends of the bar. Find the final angular velocity and the loss energy. Also find the centripetal force and centripetal acceleration of the spheres at the beginning and end.

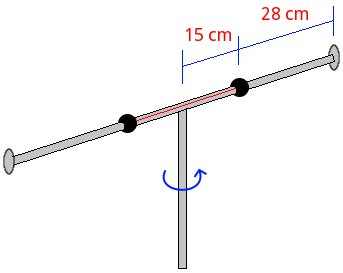
Solution with FisicaLab

Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add one element Stationary reference system, four elements Mobile with circular movement, two elements Force, one element Initial system, one element Final system, one element Energy, one element Angular momentum, two elements Angular velocity and two elements Angular acceleration. As show the image below:

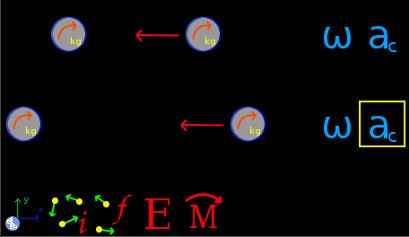
The element Stationary reference system write to default the gravity value. And the time is irrelevant for this problem. Now the two elements Mobile with circular movement at top represents the initial state of the system. Calling them Ainitial and Binitial, we have:

Name

Ainitial

m

300 @ g

vt

vtInitial

r

15 @ cm

y

0

Name

Binitial

m

300 @ g

vt

vtInitial

r

15 @ cm

y

0

Both have the same tangential speed at the beginning, which is unknown. Now with one of the elements Angular velocity, we set the initial angular velocity. You only need to do this for one of the spheres:

Object

Ainitial

vang

9

For the element Force applied to one of these spheres, that represents the centripetal force, we have:

f

centInitial

We only add one force because both spheres have the same centripetal force. Now for one of the Centripetal acceleration elements:

Object

Ainitial

ac

acInitial

Now we add these spheres to the Initial system element, which we call initial:

Name

initial

Object 1

Ainitial

Object 2

Binitial

Object 3

0

Object 4

0

Now the two elements Mobile with circular movement at bottom represents the final state of the system. Calling them Afinal and Bfinal, we have:

Name

Afinal

m

300 @ g

vt

vtFinal

r

43 @ cm

y

0

Name

Bfinal

m

300 @ g

vt

vtFinal

r

43 @ cm

y

0

Both have the same tangential speed at final. For the applied force:

f

centFinal

And to elements Angular velocity and Centripetal acceleration we have, respectively:

Object

Afinal

vang

vangFinal

Object

Afinal

ac

acFinal

Now we add these spheres to the Final system element, which we call final:

Name

final

Object 1

Afinal

Object 2

Bfinal

Object 3

0

Object 4

0

And add the elements initial and final system in the element Angular momentum, remember that there isn’t an applied moment:

System i

initial

System f

final

M

0

Also add the elements initial and final system in the element Energy:

System i

initial

System f

final

W

energy

Now click in the icon Solve to get the answer:

vangFinal = 1.095 rad/s ;  acInitial = 12.150 m/s2 ;
acFinal = 0.516 m/s2 ;  vtInitial = 1.350 m/s ;
vtFinal = 0.471 m/s ;  centInitial = 3.645 N ;
centFinal = 0.155 N ;  energy = -0.480 N*m ;
Status = success.