5.5 Information on points

Program gama-local lists separately review of coordinates of fixed and adjusted points; adjusted constrained coordinates are marked with *; see equation (3). Adjusted coordinate standard deviations m_x and m_y, and values for computing confidence intervals are given in the listing of adjusted coordinates (Parameters of statistical analysis). In the review index i is the index of unknown x_i from the system of project equations (1) corresponding to the point coordinates x and y.

Example

Fixed points
************

       point         x              y
========================================

           1  1054980.484     644498.590
           2  1054933.801     643654.101


Adjusted coordinates
********************

  i        point    approximate  correction  adjusted    std.dev conf.i.
====================== value ====== [m] ====== value ========== [mm] ===

             422
  2            x   1055167.22747  -0.00510 1055167.22237     2.7     5.4
  3            y    644041.46119   0.00023  644041.46142     2.5     5.1

             424
  4            X * 1055205.41198  -0.00056 1055205.41142     3.1     6.3
  5            Y *  644318.24425  -0.00125  644318.24300     3.6     7.2

For adjusted points, program summarizes information on standard ellipses, confidence ellipses, mean square positional errors (m_p), mean coordinate errors (m_xy) and coefficients g characterizing position of approximate coordinates with regard to the confidence ellipse.

Example

Mean errors and parameters of error ellipses
********************************************

  point     mp      mxy      mean error ellipse  conf.err. ellipse   g
========== [mm] == [mm] ==== a [mm] b  alpha[g] ==== a' [mm] b' ========

    422     3.6     2.6     2.7     2.5   187.0     6.8     6.4     0.8
    424     4.7     3.4     3.7     2.9   131.8     9.5     7.4     0.2
    403     5.7     4.0     4.3     3.6    78.9    11.0     9.3     1.1

Mean square positional error m_p and mean coordinate error (m_xy) are computed as

         m_p = sqrt(m_y^2 + m_x^2),    m_xy = m_p / sqrt(2),

where m_y^2 and m_x^2 are squares of standard deviations (variances) of adjusted points coordinates.

Semimajor and semiminor axes of standard ellipse are denoted as a and b in the listing, bearing of semimajor axis is denoted as alpha and they are computed from covariances of adjusted coordinates

         a = sqrt(1/2(cov_yy + cov_xx + c),
         b = sqrt(1/2(cov_yy + cov_xx - c),

         c = sqrt( (cov_xx - cov_yy)^2 + 4(cov_xy)^2 ),

         tan 2alpha = 2(cov_xy) / (cov_xx - cov_yy).

The angle alpha (the bearing of semimajor axis) is measured clockwise from X axis.

Probability that standard ellipse covers real position of a point is relatively low. For this reason program gama-local computes extra confidence ellipse for which the probability of covering real point position is equal to the given confidence probability. Both ellipses are located in the same center, they share the same bearing of semimajor axes and they are similar. For lengths of their semi-axis holds

         a' = k_p a,        b' = k_p b,

where k_p is a coefficient computed for the given probability P as defined in Parameters of statistical analysis.

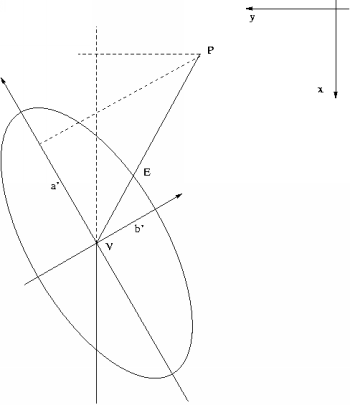
Position of approximate coordinates of an adjusted point with respect to its confidence ellipse are expressed by a coeeficient g Three cases are possible

• g < 1 approximate coordinates of adjusted point are located inside the confidence ellipse
• g = 1 approximate coordinates of adjusted point are located on the confidence ellipse
• g > 1 approximate coordinates of adjusted point are outside the confidence ellipse

The coefficient g is calculated from formula

         g = sqrt( (a_0 / a')^2 + (b_0/b')^2 )

where

         b_0 = delta_y cos(alpha) - delta_x sin(alpha),
         a_0 = delta_y sin(alpha) - delta_x cos(alpha)

symbol delta is used for correction of approximate coordinates and alpha is bearing of confidence ellipse semimajor axis.

If network contains sets of observed directions, program writes information on corresponding adjusted orientations, standard deviations and confidence intervals. Index i is the same as in the case of adjusted coordinates the index of i-th adjusted unknown in the project equations.

Example

Adjusted bearings
*****************

  i   standpoint   approximate  correction  adjusted   std.dev conf.i.
==================== value [g] ==== [g] === value [g] ======= [cc] ===

  1            1    296.484371  -0.000917  296.483454      5.1    10.3
 10            2     96.484371   0.000708   96.485079      5.1    10.4
 21          403     20.850571  -0.001953   20.848618      8.8    17.7

This document was generated on February 17, 2024 using texi2html 1.82.