6.3 Transformation from spatial to geographical coordinates

Spatial coordinates (X, Y, Z) can be easily computed from geographical ellipsoidal coordinates (B, L, H), where B is geographical latitude, L geographical longitude and H is elliposidal height, as

X = (N + H) cos B cos L
Y = (N + H) cos B sin L
Z = (N(1-e^2) + H)sin B

where N = a/sqrt(1 - e^2 sin^2 B) is the radius of curvature in the prime vertical, e^2 = (a^2 - b^2)/a^2 is the first eccentricity for the given rotational ellipsoid (spheroid) with semi-major axis a and semi-minor axis b.

In the case of coordiante transformation from (X, Y, Z) to (B, L, H), the longitude is given by the formula

tan L = Y / X.

Now we can introduce

D = sqrt(X^2 + Y^2),

so that the cartesian system become (D, Z). Coordinates B and H are then usually computed by iteration with some starting value of B_0, for example

tan B_0 = Z/D/(1 - e^2),

tan B = Z/D + N/(N+H) e^2 tan B,   H  = D / cos B = Z / sin B - N(1-e^2)

B. R. Bowring described a closed formula(3) that is more effective and sufficiantly accurate and that is used in GNU Gama.

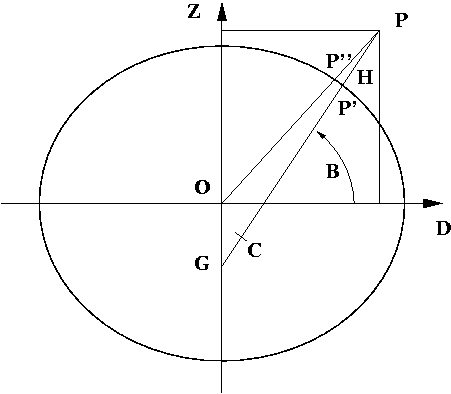
The centre of curvature C of the spheroid corresponding to P’ is the point

(e^2 a cos^3 u, -e’^2 b sin^3 u)),

where e’^2 = (a^2 - b^2)/b^2 is second eccentricity and u is the parametric latitude of the point P’, (1-e^2)N sin B = b sin u. Therefore

tan B = (Z + e’^2 b sin^3 u) / (D - e^2 a cos^3 u).

This is clearly an iterative solution; but it has been found that this formula is extremely accurate using the single first approximation for u for the tan u = (Z/D)(a/b). Maximum error in earth bound region is 3e-8 of sexagesimal arc seconds (5e-7 millimetres); maximum is 0.0018” (0.1 millimetres) at height H = 2a.

This document was generated on February 17, 2024 using texi2html 1.82.