IEEE floating-point arithmetic¶
This chapter describes functions for examining the representation of
floating point numbers and controlling the floating point environment of
your program. The functions described in this chapter are declared in
the header file gsl_ieee_utils.h.
Representation of floating point numbers¶
The IEEE Standard for Binary Floating-Point Arithmetic defines binary
formats for single and double precision numbers. Each number is composed
of three parts: a sign bit ( ), an exponent
(
), an exponent
(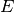 ) and a fraction (
) and a fraction (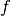 ). The numerical value of the
combination
). The numerical value of the
combination 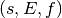 is given by the following formula,
is given by the following formula,
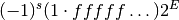
The sign bit is either zero or one. The exponent ranges from a minimum value
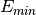 to a maximum value
to a maximum value
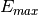 depending on the precision. The exponent is converted to an
unsigned number
depending on the precision. The exponent is converted to an
unsigned number
 , known as the biased exponent, for storage by adding a
bias parameter,
, known as the biased exponent, for storage by adding a
bias parameter,
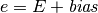
The sequence 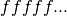 represents the digits of the binary
fraction
represents the digits of the binary
fraction 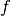 . The binary digits are stored in normalized
form, by adjusting the exponent to give a leading digit of
. The binary digits are stored in normalized
form, by adjusting the exponent to give a leading digit of 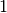 .
Since the leading digit is always 1 for normalized numbers it is
assumed implicitly and does not have to be stored.
Numbers smaller than
.
Since the leading digit is always 1 for normalized numbers it is
assumed implicitly and does not have to be stored.
Numbers smaller than
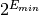 are be stored in denormalized form with a leading zero,
are be stored in denormalized form with a leading zero,
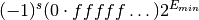
This allows gradual underflow down to
 for
for 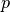 bits of precision.
A zero is encoded with the special exponent of
bits of precision.
A zero is encoded with the special exponent of
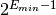 and infinities with the exponent of
and infinities with the exponent of
 .
.
The format for single precision numbers uses 32 bits divided in the following way:
seeeeeeeefffffffffffffffffffffff
s = sign bit, 1 bit
e = exponent, 8 bits (E_min=-126, E_max=127, bias=127)
f = fraction, 23 bits
The format for double precision numbers uses 64 bits divided in the following way:
seeeeeeeeeeeffffffffffffffffffffffffffffffffffffffffffffffffffff
s = sign bit, 1 bit
e = exponent, 11 bits (E_min=-1022, E_max=1023, bias=1023)
f = fraction, 52 bits
It is often useful to be able to investigate the behavior of a calculation at the bit-level and the library provides functions for printing the IEEE representations in a human-readable form.
-
void gsl_ieee_fprintf_float(FILE *stream, const float *x)¶
-
void gsl_ieee_fprintf_double(FILE *stream, const double *x)¶
These functions output a formatted version of the IEEE floating-point number pointed to by
xto the streamstream. A pointer is used to pass the number indirectly, to avoid any undesired promotion fromfloattodouble. The output takes one of the following forms,NaNthe Not-a-Number symbol
Inf, -Infpositive or negative infinity
1.fffff...*2^E, -1.fffff...*2^Ea normalized floating point number
0.fffff...*2^E, -0.fffff...*2^Ea denormalized floating point number
0, -0positive or negative zero
The output can be used directly in GNU Emacs Calc mode by preceding it with
2#to indicate binary.
-
void gsl_ieee_printf_float(const float *x)¶
-
void gsl_ieee_printf_double(const double *x)¶
These functions output a formatted version of the IEEE floating-point number pointed to by
xto the streamstdout.
The following program demonstrates the use of the functions by printing
the single and double precision representations of the fraction
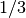 . For comparison the representation of the value promoted from
single to double precision is also printed.
. For comparison the representation of the value promoted from
single to double precision is also printed.
#include <stdio.h>
#include <gsl/gsl_ieee_utils.h>
int
main (void)
{
float f = 1.0/3.0;
double d = 1.0/3.0;
double fd = f; /* promote from float to double */
printf (" f="); gsl_ieee_printf_float(&f);
printf ("\n");
printf ("fd="); gsl_ieee_printf_double(&fd);
printf ("\n");
printf (" d="); gsl_ieee_printf_double(&d);
printf ("\n");
return 0;
}
The binary representation of 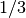 is
is 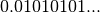 . The
output below shows that the IEEE format normalizes this fraction to give
a leading digit of 1:
. The
output below shows that the IEEE format normalizes this fraction to give
a leading digit of 1:
f= 1.01010101010101010101011*2^-2
fd= 1.0101010101010101010101100000000000000000000000000000*2^-2
d= 1.0101010101010101010101010101010101010101010101010101*2^-2
The output also shows that a single-precision number is promoted to double-precision by adding zeros in the binary representation.
Setting up your IEEE environment¶
The IEEE standard defines several modes for controlling the behavior of floating point operations. These modes specify the important properties of computer arithmetic: the direction used for rounding (e.g. whether numbers should be rounded up, down or to the nearest number), the rounding precision and how the program should handle arithmetic exceptions, such as division by zero.
Many of these features can now be controlled via standard functions such
as fpsetround(), which should be used whenever they are available.
Unfortunately in the past there has been no universal API for
controlling their behavior—each system has had its own low-level way
of accessing them. To help you write portable programs GSL allows you
to specify modes in a platform-independent way using the environment
variable GSL_IEEE_MODE. The library then takes care of all the
necessary machine-specific initializations for you when you call the
function gsl_ieee_env_setup().
-
GSL_IEEE_MODE¶
Environment variable which specifies IEEE mode.
-
void gsl_ieee_env_setup()¶
This function reads the environment variable
GSL_IEEE_MODEand attempts to set up the corresponding specified IEEE modes. The environment variable should be a list of keywords, separated by commas, like this:GSL_IEEE_MODE = "keyword, keyword, ..."
where
keywordis one of the following mode-names:single-precision double-precision extended-precision round-to-nearest round-down round-up round-to-zero mask-all mask-invalid mask-denormalized mask-division-by-zero mask-overflow mask-underflow trap-inexact trap-common
If
GSL_IEEE_MODEis empty or undefined then the function returns immediately and no attempt is made to change the system’s IEEE mode. When the modes fromGSL_IEEE_MODEare turned on the function prints a short message showing the new settings to remind you that the results of the program will be affected.If the requested modes are not supported by the platform being used then the function calls the error handler and returns an error code of
GSL_EUNSUP.When options are specified using this method, the resulting mode is based on a default setting of the highest available precision (double precision or extended precision, depending on the platform) in round-to-nearest mode, with all exceptions enabled apart from the INEXACT exception. The INEXACT exception is generated whenever rounding occurs, so it must generally be disabled in typical scientific calculations. All other floating-point exceptions are enabled by default, including underflows and the use of denormalized numbers, for safety. They can be disabled with the individual
mask-settings or together usingmask-all.The following adjusted combination of modes is convenient for many purposes:
GSL_IEEE_MODE="double-precision,"\ "mask-underflow,"\ "mask-denormalized"
This choice ignores any errors relating to small numbers (either denormalized, or underflowing to zero) but traps overflows, division by zero and invalid operations.
Note that on the x86 series of processors this function sets both the original x87 mode and the newer MXCSR mode, which controls SSE floating-point operations. The SSE floating-point units do not have a precision-control bit, and always work in double-precision. The single-precision and extended-precision keywords have no effect in this case.
To demonstrate the effects of different rounding modes consider the
following program which computes  , the base of natural
logarithms, by summing a rapidly-decreasing series,
, the base of natural
logarithms, by summing a rapidly-decreasing series,
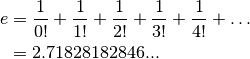
#include <stdio.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_ieee_utils.h>
int
main (void)
{
double x = 1, oldsum = 0, sum = 0;
int i = 0;
gsl_ieee_env_setup (); /* read GSL_IEEE_MODE */
do
{
i++;
oldsum = sum;
sum += x;
x = x / i;
printf ("i=%2d sum=%.18f error=%g\n",
i, sum, sum - M_E);
if (i > 30)
break;
}
while (sum != oldsum);
return 0;
}
Here are the results of running the program in round-to-nearest
mode. This is the IEEE default so it isn’t really necessary to specify
it here:
$ GSL_IEEE_MODE="round-to-nearest" ./a.out
i= 1 sum=1.000000000000000000 error=-1.71828
i= 2 sum=2.000000000000000000 error=-0.718282
....
i=18 sum=2.718281828459045535 error=4.44089e-16
i=19 sum=2.718281828459045535 error=4.44089e-16
After nineteen terms the sum converges to within 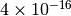 of the correct value.
If we now change the rounding mode to
of the correct value.
If we now change the rounding mode to
round-down the final result is less accurate:
$ GSL_IEEE_MODE="round-down" ./a.out
i= 1 sum=1.000000000000000000 error=-1.71828
....
i=19 sum=2.718281828459041094 error=-3.9968e-15
The result is about
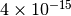 below the correct value, an order of magnitude worse than the result
obtained in the
below the correct value, an order of magnitude worse than the result
obtained in the round-to-nearest mode.
If we change to rounding mode to round-up then the final result
is higher than the correct value (when we add each term to the sum the
final result is always rounded up, which increases the sum by at least
one tick until the added term underflows to zero). To avoid this
problem we would need to use a safer converge criterion, such as
while (fabs(sum - oldsum) > epsilon), with a suitably chosen
value of epsilon.
Finally we can see the effect of computing the sum using
single-precision rounding, in the default round-to-nearest
mode. In this case the program thinks it is still using double precision
numbers but the CPU rounds the result of each floating point operation
to single-precision accuracy. This simulates the effect of writing the
program using single-precision float variables instead of
double variables. The iteration stops after about half the number
of iterations and the final result is much less accurate:
$ GSL_IEEE_MODE="single-precision" ./a.out
....
i=12 sum=2.718281984329223633 error=1.5587e-07
with an error of
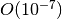 ,
which corresponds to single
precision accuracy (about 1 part in
,
which corresponds to single
precision accuracy (about 1 part in 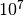 ). Continuing the
iterations further does not decrease the error because all the
subsequent results are rounded to the same value.
). Continuing the
iterations further does not decrease the error because all the
subsequent results are rounded to the same value.
References and Further Reading¶
The reference for the IEEE standard is,
ANSI/IEEE Std 754-1985, IEEE Standard for Binary Floating-Point Arithmetic.
A more pedagogical introduction to the standard can be found in the following paper,
David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic. ACM Computing Surveys, Vol.: 23, No.: 1 (March 1991), pages 5–48.
Corrigendum: ACM Computing Surveys, Vol.: 23, No.: 3 (September 1991), page 413. and see also the sections by B. A. Wichmann and Charles B. Dunham in Surveyor’s Forum: “What Every Computer Scientist Should Know About Floating-Point Arithmetic”. ACM Computing Surveys, Vol.: 24, No.: 3 (September 1992), page 319.
A detailed textbook on IEEE arithmetic and its practical use is available from SIAM Press,
Michael L. Overton, Numerical Computing with IEEE Floating Point Arithmetic, SIAM Press, ISBN 0898715717.