Random Number Generation¶
The library provides a large collection of random number generators which can be accessed through a uniform interface. Environment variables allow you to select different generators and seeds at runtime, so that you can easily switch between generators without needing to recompile your program. Each instance of a generator keeps track of its own state, allowing the generators to be used in multi-threaded programs. Additional functions are available for transforming uniform random numbers into samples from continuous or discrete probability distributions such as the Gaussian, log-normal or Poisson distributions.
These functions are declared in the header file gsl_rng.h.
General comments on random numbers¶
In 1988, Park and Miller wrote a paper entitled “Random number generators: good ones are hard to find.” [Commun.: ACM, 31, 1192–1201]. Fortunately, some excellent random number generators are available, though poor ones are still in common use. You may be happy with the system-supplied random number generator on your computer, but you should be aware that as computers get faster, requirements on random number generators increase. Nowadays, a simulation that calls a random number generator millions of times can often finish before you can make it down the hall to the coffee machine and back.
A very nice review of random number generators was written by Pierre L’Ecuyer, as Chapter 4 of the book: Handbook on Simulation, Jerry Banks, ed. (Wiley, 1997). The chapter is available in postscript from L’Ecuyer’s ftp site (see references). Knuth’s volume on Seminumerical Algorithms (originally published in 1968) devotes 170 pages to random number generators, and has recently been updated in its 3rd edition (1997). It is brilliant, a classic. If you don’t own it, you should stop reading right now, run to the nearest bookstore, and buy it.
A good random number generator will satisfy both theoretical and statistical properties. Theoretical properties are often hard to obtain (they require real math!), but one prefers a random number generator with a long period, low serial correlation, and a tendency not to “fall mainly on the planes.” Statistical tests are performed with numerical simulations. Generally, a random number generator is used to estimate some quantity for which the theory of probability provides an exact answer. Comparison to this exact answer provides a measure of “randomness”.
The Random Number Generator Interface¶
It is important to remember that a random number generator is not a “real” function like sine or cosine. Unlike real functions, successive calls to a random number generator yield different return values. Of course that is just what you want for a random number generator, but to achieve this effect, the generator must keep track of some kind of “state” variable. Sometimes this state is just an integer (sometimes just the value of the previously generated random number), but often it is more complicated than that and may involve a whole array of numbers, possibly with some indices thrown in. To use the random number generators, you do not need to know the details of what comprises the state, and besides that varies from algorithm to algorithm.
-
type gsl_rng_type¶
-
type gsl_rng¶
The random number generator library uses two special structs,
gsl_rng_typewhich holds static information about each type of generator andgsl_rngwhich describes an instance of a generator created from a givengsl_rng_type.
The functions described in this section are declared in the header file
gsl_rng.h.
Random number generator initialization¶
-
gsl_rng *gsl_rng_alloc(const gsl_rng_type *T)¶
This function returns a pointer to a newly-created instance of a random number generator of type
T. For example, the following code creates an instance of the Tausworthe generator:gsl_rng * r = gsl_rng_alloc (gsl_rng_taus);
If there is insufficient memory to create the generator then the function returns a null pointer and the error handler is invoked with an error code of
GSL_ENOMEM.The generator is automatically initialized with the default seed,
gsl_rng_default_seed. This is zero by default but can be changed either directly or by using the environment variableGSL_RNG_SEED.The details of the available generator types are described later in this chapter.
-
void gsl_rng_set(const gsl_rng *r, unsigned long int s)¶
This function initializes (or “seeds”) the random number generator. If the generator is seeded with the same value of
son two different runs, the same stream of random numbers will be generated by successive calls to the routines below. If different values of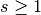 are supplied, then the generated streams of random
numbers should be completely different. If the seed
are supplied, then the generated streams of random
numbers should be completely different. If the seed sis zero then the standard seed from the original implementation is used instead. For example, the original Fortran source code for theranluxgenerator used a seed of 314159265, and so choosingsequal to zero reproduces this when usinggsl_rng_ranlux.When using multiple seeds with the same generator, choose seed values greater than zero to avoid collisions with the default setting.
Note that the most generators only accept 32-bit seeds, with higher values being reduced modulo
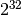 .
For generators with smaller ranges the maximum seed value will typically be lower.
.
For generators with smaller ranges the maximum seed value will typically be lower.
Sampling from a random number generator¶
The following functions return uniformly distributed random numbers,
either as integers or double precision floating point numbers. Inline versions of these functions are used when HAVE_INLINE is defined.
To obtain non-uniform distributions, see Random Number Distributions.
-
unsigned long int gsl_rng_get(const gsl_rng *r)¶
This function returns a random integer from the generator
r. The minimum and maximum values depend on the algorithm used, but all integers in the range [min,max] are equally likely. The values ofminandmaxcan be determined using the auxiliary functionsgsl_rng_max()andgsl_rng_min().
-
double gsl_rng_uniform(const gsl_rng *r)¶
This function returns a double precision floating point number uniformly distributed in the range [0,1). The range includes 0.0 but excludes 1.0. The value is typically obtained by dividing the result of
gsl_rng_get(r)bygsl_rng_max(r) + 1.0in double precision. Some generators compute this ratio internally so that they can provide floating point numbers with more than 32 bits of randomness (the maximum number of bits that can be portably represented in a singleunsigned long int).
-
double gsl_rng_uniform_pos(const gsl_rng *r)¶
This function returns a positive double precision floating point number uniformly distributed in the range (0,1), excluding both 0.0 and 1.0. The number is obtained by sampling the generator with the algorithm of
gsl_rng_uniform()until a non-zero value is obtained. You can use this function if you need to avoid a singularity at 0.0.
-
unsigned long int gsl_rng_uniform_int(const gsl_rng *r, unsigned long int n)¶
This function returns a random integer from 0 to
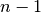 inclusive
by scaling down and/or discarding samples from the generator
inclusive
by scaling down and/or discarding samples from the generator r. All integers in the range![[0,n-1]](_images/math/edb4a7fb07fa73cdae2a073bc507db8cef3dfbe8.png) are produced with equal
probability. For generators with a non-zero minimum value an offset
is applied so that zero is returned with the correct probability.
are produced with equal
probability. For generators with a non-zero minimum value an offset
is applied so that zero is returned with the correct probability.Note that this function is designed for sampling from ranges smaller than the range of the underlying generator. The parameter
nmust be less than or equal to the range of the generatorr. Ifnis larger than the range of the generator then the function calls the error handler with an error code ofGSL_EINVALand returns zero.In particular, this function is not intended for generating the full range of unsigned integer values
![[0,2^{32}-1]](_images/math/4aebd369e5e4d76268f3740c38ce02bb179998f8.png) .
Instead choose a generator with the maximal integer range and zero minimum
value, such as
.
Instead choose a generator with the maximal integer range and zero minimum
value, such as gsl_rng_ranlxd1,gsl_rng_mt19937orgsl_rng_taus, and sample it directly usinggsl_rng_get(). The range of each generator can be found using the auxiliary functions described in the next section.
Auxiliary random number generator functions¶
The following functions provide information about an existing generator. You should use them in preference to hard-coding the generator parameters into your own code.
-
const char *gsl_rng_name(const gsl_rng *r)¶
This function returns a pointer to the name of the generator. For example:
printf ("r is a '%s' generator\n", gsl_rng_name (r));
would print something like:
r is a 'taus' generator
-
unsigned long int gsl_rng_max(const gsl_rng *r)¶
This function returns the largest value that
gsl_rng_get()can return.
-
unsigned long int gsl_rng_min(const gsl_rng *r)¶
This function returns the smallest value that
gsl_rng_get()can return. Usually this value is zero. There are some generators with algorithms that cannot return zero, and for these generators the minimum value is 1.
-
void *gsl_rng_state(const gsl_rng *r)¶
-
size_t gsl_rng_size(const gsl_rng *r)¶
These functions return a pointer to the state of generator
rand its size. You can use this information to access the state directly. For example, the following code will write the state of a generator to a stream:void * state = gsl_rng_state (r); size_t n = gsl_rng_size (r); fwrite (state, n, 1, stream);
-
const gsl_rng_type **gsl_rng_types_setup(void)¶
This function returns a pointer to an array of all the available generator types, terminated by a null pointer. The function should be called once at the start of the program, if needed. The following code fragment shows how to iterate over the array of generator types to print the names of the available algorithms:
const gsl_rng_type **t, **t0; t0 = gsl_rng_types_setup (); printf ("Available generators:\n"); for (t = t0; *t != 0; t++) { printf ("%s\n", (*t)->name); }
Random number environment variables¶
The library allows you to choose a default generator and seed from the
environment variables GSL_RNG_TYPE and GSL_RNG_SEED and
the function gsl_rng_env_setup(). This makes it easy try out
different generators and seeds without having to recompile your program.
-
GSL_RNG_TYPE¶
This environment variable specifies the default random number generator. It should be the name of a generator, such as
tausormt19937.
-
GSL_RNG_SEED¶
This environment variable specifies the default seed for the random number generator
-
gsl_rng_type *gsl_rng_default¶
This global library variable specifies the default random number generator, and can be initialized from
GSL_RNG_TYPEusinggsl_rng_env_setup(). It is defined as follows:extern const gsl_rng_type *gsl_rng_default
-
unsigned long int gsl_rng_default_seed¶
This global library variable specifies the seed for the default random number generator, and can be initialized from
GSL_RNG_SEEDusinggsl_rng_env_setup(). It is set to zero by default and is defined as follows:extern unsigned long int gsl_rng_default_seed
-
const gsl_rng_type *gsl_rng_env_setup(void)¶
This function reads the environment variables
GSL_RNG_TYPEandGSL_RNG_SEEDand uses their values to set the corresponding library variablesgsl_rng_defaultandgsl_rng_default_seed.The value of
GSL_RNG_SEEDis converted to anunsigned long intusing the C library functionstrtoul().If you don’t specify a generator for
GSL_RNG_TYPEthengsl_rng_mt19937is used as the default. The initial value ofgsl_rng_default_seedis zero.
Here is a short program which shows how to create a global
generator using the environment variables GSL_RNG_TYPE and
GSL_RNG_SEED,
#include <stdio.h>
#include <gsl/gsl_rng.h>
gsl_rng * r; /* global generator */
int
main (void)
{
const gsl_rng_type * T;
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc (T);
printf ("generator type: %s\n", gsl_rng_name (r));
printf ("seed = %lu\n", gsl_rng_default_seed);
printf ("first value = %lu\n", gsl_rng_get (r));
gsl_rng_free (r);
return 0;
}
Running the program without any environment variables uses the initial
defaults, an mt19937 generator with a seed of 0,
generator type: mt19937
seed = 0
first value = 4293858116
By setting the two variables on the command line we can change the default generator and the seed:
$ GSL_RNG_TYPE="taus" GSL_RNG_SEED=123 ./a.out
GSL_RNG_TYPE=taus
GSL_RNG_SEED=123
generator type: taus
seed = 123
first value = 2720986350
Copying random number generator state¶
The above methods do not expose the random number state which changes from call to call. It is often useful to be able to save and restore the state. To permit these practices, a few somewhat more advanced functions are supplied. These include:
Reading and writing random number generator state¶
The library provides functions for reading and writing the random number state to a file as binary data.
-
int gsl_rng_fwrite(FILE *stream, const gsl_rng *r)¶
This function writes the random number state of the random number generator
rto the streamstreamin binary format. The return value is 0 for success andGSL_EFAILEDif there was a problem writing to the file. Since the data is written in the native binary format it may not be portable between different architectures.
-
int gsl_rng_fread(FILE *stream, gsl_rng *r)¶
This function reads the random number state into the random number generator
rfrom the open streamstreamin binary format. The random number generatorrmust be preinitialized with the correct random number generator type since type information is not saved. The return value is 0 for success andGSL_EFAILEDif there was a problem reading from the file. The data is assumed to have been written in the native binary format on the same architecture.
Random number generator algorithms¶
The functions described above make no reference to the actual algorithm used. This is deliberate so that you can switch algorithms without having to change any of your application source code. The library provides a large number of generators of different types, including simulation quality generators, generators provided for compatibility with other libraries and historical generators from the past.
The following generators are recommended for use in simulation. They have extremely long periods, low correlation and pass most statistical tests. For the most reliable source of uncorrelated numbers, the second-generation RANLUX generators have the strongest proof of randomness.
-
gsl_rng_type *gsl_rng_mt19937¶
The MT19937 generator of Makoto Matsumoto and Takuji Nishimura is a variant of the twisted generalized feedback shift-register algorithm, and is known as the “Mersenne Twister” generator. It has a Mersenne prime period of
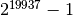 (about
(about 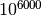 ) and is
equi-distributed in 623 dimensions. It has passed the DIEHARD
statistical tests. It uses 624 words of state per generator and is
comparable in speed to the other generators. The original generator used
a default seed of 4357 and choosing
) and is
equi-distributed in 623 dimensions. It has passed the DIEHARD
statistical tests. It uses 624 words of state per generator and is
comparable in speed to the other generators. The original generator used
a default seed of 4357 and choosing sequal to zero ingsl_rng_set()reproduces this. Later versions switched to 5489 as the default seed, you can choose this explicitly viagsl_rng_set()instead if you require it.For more information see,
Makoto Matsumoto and Takuji Nishimura, “Mersenne Twister: A 623-dimensionally equidistributed uniform pseudorandom number generator”. ACM Transactions on Modeling and Computer Simulation, Vol.: 8, No.: 1 (Jan. 1998), Pages 3–30
The generator
gsl_rng_mt19937uses the second revision of the seeding procedure published by the two authors above in 2002. The original seeding procedures could cause spurious artifacts for some seed values. They are still available through the alternative generatorsgsl_rng_mt19937_1999andgsl_rng_mt19937_1998.
-
gsl_rng_type *gsl_rng_ranlxs0¶
-
gsl_rng_type *gsl_rng_ranlxs1¶
-
gsl_rng_type *gsl_rng_ranlxs2¶
The generator
ranlxs0is a second-generation version of the RANLUX algorithm of Luscher, which produces “luxury random numbers”. This generator provides single precision output (24 bits) at three luxury levelsranlxs0,ranlxs1andranlxs2, in increasing order of strength. It uses double-precision floating point arithmetic internally and can be significantly faster than the integer version ofranlux, particularly on 64-bit architectures. The period of the generator is about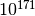 .
The algorithm has mathematically proven properties and
can provide truly decorrelated numbers at a known level of randomness.
The higher luxury levels provide increased decorrelation between samples
as an additional safety margin.
.
The algorithm has mathematically proven properties and
can provide truly decorrelated numbers at a known level of randomness.
The higher luxury levels provide increased decorrelation between samples
as an additional safety margin.Note that the range of allowed seeds for this generator is
![[0,2^{31}-1]](_images/math/be126fc66bfcd48a626f5c2be119ab06c77ab55b.png) .
Higher seed values are wrapped modulo
.
Higher seed values are wrapped modulo 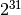 .
.
-
gsl_rng_type *gsl_rng_ranlxd1¶
-
gsl_rng_type *gsl_rng_ranlxd2¶
These generators produce double precision output (48 bits) from the RANLXS generator. The library provides two luxury levels
ranlxd1andranlxd2, in increasing order of strength.
-
gsl_rng_type *gsl_rng_ranlux¶
-
gsl_rng_type *gsl_rng_ranlux389¶
The
ranluxgenerator is an implementation of the original algorithm developed by Luscher. It uses a lagged-fibonacci-with-skipping algorithm to produce “luxury random numbers”. It is a 24-bit generator, originally designed for single-precision IEEE floating point numbers. This implementation is based on integer arithmetic, while the second-generation versions RANLXS and RANLXD described above provide floating-point implementations which will be faster on many platforms. The period of the generator is about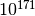 .
The algorithm has mathematically proven properties and
it can provide truly decorrelated numbers at a known level of
randomness. The default level of decorrelation recommended by Luscher
is provided by
.
The algorithm has mathematically proven properties and
it can provide truly decorrelated numbers at a known level of
randomness. The default level of decorrelation recommended by Luscher
is provided by gsl_rng_ranlux, whilegsl_rng_ranlux389gives the highest level of randomness, with all 24 bits decorrelated. Both types of generator use 24 words of state per generator.For more information see,
M. Luscher, “A portable high-quality random number generator for lattice field theory calculations”, Computer Physics Communications, 79 (1994) 100–110.
F. James, “RANLUX: A Fortran implementation of the high-quality pseudo-random number generator of Luscher”, Computer Physics Communications, 79 (1994) 111–114
-
gsl_rng_type *gsl_rng_cmrg¶
This is a combined multiple recursive generator by L’Ecuyer. Its sequence is,
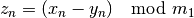
where the two underlying generators
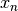 and
and 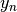 are,
are,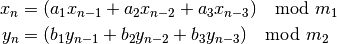
with coefficients
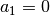 ,
,
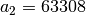 ,
,
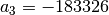 ,
,
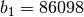 ,
,
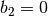 ,
,
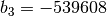 ,
and moduli
,
and moduli
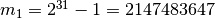 and
and
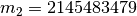 .
.The period of this generator is
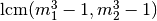 ,
which is approximately
,
which is approximately
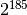 (about
(about 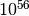 ).
It uses 6 words of state per generator. For more information see,
).
It uses 6 words of state per generator. For more information see,P. L’Ecuyer, “Combined Multiple Recursive Random Number Generators”, Operations Research, 44, 5 (1996), 816–822.
-
gsl_rng_type *gsl_rng_mrg¶
This is a fifth-order multiple recursive generator by L’Ecuyer, Blouin and Coutre. Its sequence is,
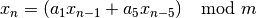
with
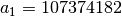 ,
,
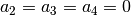 ,
,
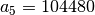 and
and
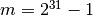 .
.The period of this generator is about
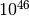 .
It uses 5 words
of state per generator. More information can be found in the following
paper,
.
It uses 5 words
of state per generator. More information can be found in the following
paper,P. L’Ecuyer, F. Blouin, and R. Coutre, “A search for good multiple recursive random number generators”, ACM Transactions on Modeling and Computer Simulation 3, 87–98 (1993).
-
gsl_rng_type *gsl_rng_taus¶
-
gsl_rng_type *gsl_rng_taus2¶
This is a maximally equidistributed combined Tausworthe generator by L’Ecuyer. The sequence is,
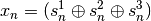
where,
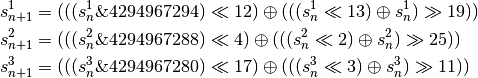
computed modulo
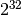 .
In the formulas above
.
In the formulas above
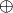 denotes exclusive-or. Note that the algorithm relies on the properties
of 32-bit unsigned integers and has been implemented using a bitmask
of
denotes exclusive-or. Note that the algorithm relies on the properties
of 32-bit unsigned integers and has been implemented using a bitmask
of 0xFFFFFFFFto make it work on 64 bit machines.The period of this generator is
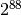 (about
(about 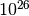 ).
It uses 3 words of state per generator. For more
information see,
).
It uses 3 words of state per generator. For more
information see,P. L’Ecuyer, “Maximally Equidistributed Combined Tausworthe Generators”, Mathematics of Computation, 65, 213 (1996), 203–213.
The generator
gsl_rng_taus2uses the same algorithm asgsl_rng_tausbut with an improved seeding procedure described in the paper,P. L’Ecuyer, “Tables of Maximally Equidistributed Combined LFSR Generators”, Mathematics of Computation, 68, 225 (1999), 261–269
The generator
gsl_rng_taus2should now be used in preference togsl_rng_taus.
-
gsl_rng_type *gsl_rng_gfsr4¶
The
gfsr4generator is like a lagged-fibonacci generator, and produces each number as anxor’d sum of four previous values.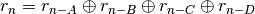
Ziff (ref below) notes that “it is now widely known” that two-tap registers (such as R250, which is described below) have serious flaws, the most obvious one being the three-point correlation that comes from the definition of the generator. Nice mathematical properties can be derived for GFSR’s, and numerics bears out the claim that 4-tap GFSR’s with appropriately chosen offsets are as random as can be measured, using the author’s test.
This implementation uses the values suggested the example on p392 of Ziff’s article:
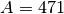 ,
, 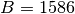 ,
, 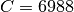 ,
, 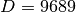 .
.If the offsets are appropriately chosen (such as the one ones in this implementation), then the sequence is said to be maximal; that means that the period is
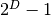 , where
, where 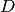 is the longest lag.
(It is one less than
is the longest lag.
(It is one less than 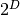 because it is not permitted to have all
zeros in the
because it is not permitted to have all
zeros in the ra[]array.) For this implementation with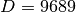 that works out to about
that works out to about 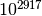 .
.Note that the implementation of this generator using a 32-bit integer amounts to 32 parallel implementations of one-bit generators. One consequence of this is that the period of this 32-bit generator is the same as for the one-bit generator. Moreover, this independence means that all 32-bit patterns are equally likely, and in particular that 0 is an allowed random value. (We are grateful to Heiko Bauke for clarifying for us these properties of GFSR random number generators.)
For more information see,
Robert M. Ziff, “Four-tap shift-register-sequence random-number generators”, Computers in Physics, 12(4), Jul/Aug 1998, pp 385–392.
Unix random number generators¶
The standard Unix random number generators rand, random
and rand48 are provided as part of GSL. Although these
generators are widely available individually often they aren’t all
available on the same platform. This makes it difficult to write
portable code using them and so we have included the complete set of
Unix generators in GSL for convenience. Note that these generators
don’t produce high-quality randomness and aren’t suitable for work
requiring accurate statistics. However, if you won’t be measuring
statistical quantities and just want to introduce some variation into
your program then these generators are quite acceptable.
-
gsl_rng_type *gsl_rng_rand¶
This is the BSD
randgenerator. Its sequence is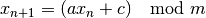
with
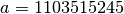 ,
,
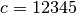 and
and
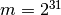 .
The seed specifies the initial value,
.
The seed specifies the initial value,
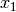 . The period of this
generator is
. The period of this
generator is
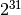 ,
and it uses 1 word of storage per generator.
,
and it uses 1 word of storage per generator.
-
gsl_rng_type *gsl_rng_random_bsd¶
-
gsl_rng_type *gsl_rng_random_libc5¶
-
gsl_rng_type *gsl_rng_random_glibc2¶
These generators implement the
randomfamily of functions, a set of linear feedback shift register generators originally used in BSD Unix. There are several versions ofrandomin use today: the original BSD version (e.g. on SunOS4), a libc5 version (found on older GNU/Linux systems) and a glibc2 version. Each version uses a different seeding procedure, and thus produces different sequences.The original BSD routines accepted a variable length buffer for the generator state, with longer buffers providing higher-quality randomness. The
randomfunction implemented algorithms for buffer lengths of 8, 32, 64, 128 and 256 bytes, and the algorithm with the largest length that would fit into the user-supplied buffer was used. To support these algorithms additional generators are available with the following names:gsl_rng_random8_bsd gsl_rng_random32_bsd gsl_rng_random64_bsd gsl_rng_random128_bsd gsl_rng_random256_bsd
where the numeric suffix indicates the buffer length. The original BSD
randomfunction used a 128-byte default buffer and sogsl_rng_random_bsdhas been made equivalent togsl_rng_random128_bsd. Corresponding versions of thelibc5andglibc2generators are also available, with the namesgsl_rng_random8_libc5,gsl_rng_random8_glibc2, etc.
-
gsl_rng_type *gsl_rng_rand48¶
This is the Unix
rand48generator. Its sequence is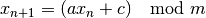
defined on 48-bit unsigned integers with
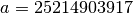 ,
,
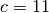 and
and
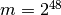 .
The seed specifies the upper 32 bits of the initial value,
.
The seed specifies the upper 32 bits of the initial value, 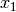 ,
with the lower 16 bits set to
,
with the lower 16 bits set to 0x330E. The functiongsl_rng_get()returns the upper 32 bits from each term of the sequence. This does not have a direct parallel in the originalrand48functions, but forcing the result to typelong intreproduces the output ofmrand48. The functiongsl_rng_uniform()uses the full 48 bits of internal state to return the double precision number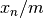 , which is equivalent to the
function
, which is equivalent to the
function drand48. Note that some versions of the GNU C Library contained a bug inmrand48function which caused it to produce different results (only the lower 16-bits of the return value were set).
Other random number generators¶
The generators in this section are provided for compatibility with existing libraries. If you are converting an existing program to use GSL then you can select these generators to check your new implementation against the original one, using the same random number generator. After verifying that your new program reproduces the original results you can then switch to a higher-quality generator.
Note that most of the generators in this section are based on single
linear congruence relations, which are the least sophisticated type of
generator. In particular, linear congruences have poor properties when
used with a non-prime modulus, as several of these routines do (e.g.
with a power of two modulus,
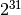 or
or
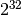 ).
This leads to periodicity in the least significant bits of each number,
with only the higher bits having any randomness. Thus if you want to
produce a random bitstream it is best to avoid using the least
significant bits.
).
This leads to periodicity in the least significant bits of each number,
with only the higher bits having any randomness. Thus if you want to
produce a random bitstream it is best to avoid using the least
significant bits.
-
gsl_rng_type *gsl_rng_ranf¶
This is the CRAY random number generator
RANF. Its sequence is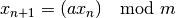
defined on 48-bit unsigned integers with
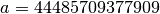 and
and
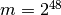 .
The seed specifies the lower 32 bits of the initial value,
.
The seed specifies the lower 32 bits of the initial value,
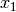 , with the lowest bit set to
prevent the seed taking an even value. The upper 16 bits of
, with the lowest bit set to
prevent the seed taking an even value. The upper 16 bits of
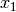 are set to 0. A consequence of this procedure is that the pairs of seeds
2 and 3, 4 and 5, etc.: produce the same sequences.
are set to 0. A consequence of this procedure is that the pairs of seeds
2 and 3, 4 and 5, etc.: produce the same sequences.The generator compatible with the CRAY MATHLIB routine RANF. It produces double precision floating point numbers which should be identical to those from the original RANF.
There is a subtlety in the implementation of the seeding. The initial state is reversed through one step, by multiplying by the modular inverse of
 mod
mod  . This is done for compatibility with
the original CRAY implementation.
. This is done for compatibility with
the original CRAY implementation.Note that you can only seed the generator with integers up to
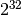 ,
while the original CRAY implementation uses
non-portable wide integers which can cover all
,
while the original CRAY implementation uses
non-portable wide integers which can cover all
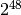 states of the generator.
states of the generator.The function
gsl_rng_get()returns the upper 32 bits from each term of the sequence. The functiongsl_rng_uniform()uses the full 48 bits to return the double precision number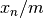 .
.The period of this generator is
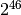 .
.
-
gsl_rng_type *gsl_rng_ranmar¶
This is the RANMAR lagged-fibonacci generator of Marsaglia, Zaman and Tsang. It is a 24-bit generator, originally designed for single-precision IEEE floating point numbers. It was included in the CERNLIB high-energy physics library.
-
gsl_rng_type *gsl_rng_r250¶
This is the shift-register generator of Kirkpatrick and Stoll. The sequence is based on the recurrence
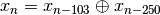
where
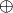 denotes exclusive-or, defined on
32-bit words. The period of this generator is about
denotes exclusive-or, defined on
32-bit words. The period of this generator is about 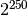 and it
uses 250 words of state per generator.
and it
uses 250 words of state per generator.For more information see,
S. Kirkpatrick and E. Stoll, “A very fast shift-register sequence random number generator”, Journal of Computational Physics, 40, 517–526 (1981)
-
gsl_rng_type *gsl_rng_tt800¶
This is an earlier version of the twisted generalized feedback shift-register generator, and has been superseded by the development of MT19937. However, it is still an acceptable generator in its own right. It has a period of
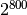 and uses 33 words of storage per generator.
and uses 33 words of storage per generator.For more information see,
Makoto Matsumoto and Yoshiharu Kurita, “Twisted GFSR Generators II”, ACM Transactions on Modelling and Computer Simulation, Vol.: 4, No.: 3, 1994, pages 254–266.
-
gsl_rng_type *gsl_rng_vax¶
This is the VAX generator
MTH$RANDOM. Its sequence is,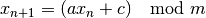
with
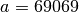 ,
, 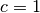 and
and
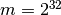 .
The seed specifies the initial value,
.
The seed specifies the initial value,
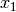 . The
period of this generator is
. The
period of this generator is
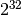 and it uses 1 word of storage per
generator.
and it uses 1 word of storage per
generator.
-
gsl_rng_type *gsl_rng_transputer¶
This is the random number generator from the INMOS Transputer Development system. Its sequence is,
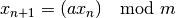
with
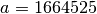 and
and
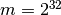 .
The seed specifies the initial value,
.
The seed specifies the initial value,
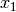 .
.
-
gsl_rng_type *gsl_rng_randu¶
This is the IBM
RANDUgenerator. Its sequence is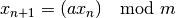
with
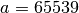 and
and
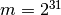 . The
seed specifies the initial value,
. The
seed specifies the initial value,
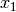 . The period of this
generator was only
. The period of this
generator was only
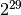 .
It has become a textbook example of a poor generator.
.
It has become a textbook example of a poor generator.
-
gsl_rng_type *gsl_rng_minstd¶
This is Park and Miller’s “minimal standard” MINSTD generator, a simple linear congruence which takes care to avoid the major pitfalls of such algorithms. Its sequence is,
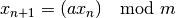
with
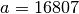 and
and
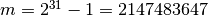 .
The seed specifies the initial value,
.
The seed specifies the initial value,
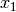 . The period of this
generator is about
. The period of this
generator is about
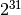 .
.This generator was used in the IMSL Library (subroutine RNUN) and in MATLAB (the RAND function) in the past. It is also sometimes known by the acronym “GGL” (I’m not sure what that stands for).
For more information see,
Park and Miller, “Random Number Generators: Good ones are hard to find”, Communications of the ACM, October 1988, Volume 31, No 10, pages 1192–1201.
-
gsl_rng_type *gsl_rng_uni¶
-
gsl_rng_type *gsl_rng_uni32¶
This is a reimplementation of the 16-bit SLATEC random number generator RUNIF. A generalization of the generator to 32 bits is provided by
gsl_rng_uni32. The original source code is available from NETLIB.
-
gsl_rng_type *gsl_rng_slatec¶
This is the SLATEC random number generator RAND. It is ancient. The original source code is available from NETLIB.
-
gsl_rng_type *gsl_rng_zuf¶
This is the ZUFALL lagged Fibonacci series generator of Peterson. Its sequence is,
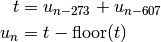
The original source code is available from NETLIB. For more information see,
W. Petersen, “Lagged Fibonacci Random Number Generators for the NEC SX-3”, International Journal of High Speed Computing (1994).
-
gsl_rng_type *gsl_rng_knuthran2¶
This is a second-order multiple recursive generator described by Knuth in Seminumerical Algorithms, 3rd Ed., page 108. Its sequence is,
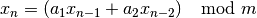
with
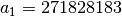 ,
,
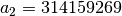 ,
and
,
and
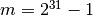 .
.
-
gsl_rng_type *gsl_rng_knuthran2002¶
-
gsl_rng_type *gsl_rng_knuthran¶
This is a second-order multiple recursive generator described by Knuth in Seminumerical Algorithms, 3rd Ed., Section 3.6. Knuth provides its C code. The updated routine
gsl_rng_knuthran2002is from the revised 9th printing and corrects some weaknesses in the earlier version, which is implemented asgsl_rng_knuthran.
-
gsl_rng_type *gsl_rng_borosh13¶
-
gsl_rng_type *gsl_rng_fishman18¶
-
gsl_rng_type *gsl_rng_fishman20¶
-
gsl_rng_type *gsl_rng_lecuyer21¶
-
gsl_rng_type *gsl_rng_waterman14¶
These multiplicative generators are taken from Knuth’s Seminumerical Algorithms, 3rd Ed., pages 106–108. Their sequence is,
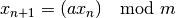
where the seed specifies the initial value,
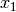 .
The parameters
.
The parameters  and
and  are as follows,
Borosh-Niederreiter:
are as follows,
Borosh-Niederreiter:
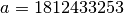 ,
, 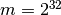 ,
Fishman18:
,
Fishman18:
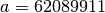 ,
,
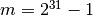 ,
Fishman20:
,
Fishman20:
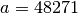 ,
,
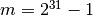 ,
L’Ecuyer:
,
L’Ecuyer:
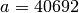 ,
,
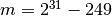 ,
Waterman:
,
Waterman:
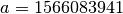 ,
,
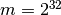 .
.
-
gsl_rng_type *gsl_rng_fishman2x¶
This is the L’Ecuyer–Fishman random number generator. It is taken from Knuth’s Seminumerical Algorithms, 3rd Ed., page 108. Its sequence is,
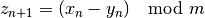
with
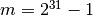 .
.
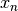 and
and 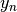 are given by the
are given by the fishman20andlecuyer21algorithms. The seed specifies the initial value,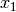 .
.
-
gsl_rng_type *gsl_rng_coveyou¶
This is the Coveyou random number generator. It is taken from Knuth’s Seminumerical Algorithms, 3rd Ed., Section 3.2.2. Its sequence is,
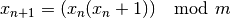
with
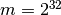 .
The seed specifies the initial value,
.
The seed specifies the initial value,
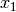 .
.
Performance¶
The following table shows the relative performance of a selection the
available random number generators. The fastest simulation quality
generators are taus, gfsr4 and mt19937. The
generators which offer the best mathematically-proven quality are those
based on the RANLUX algorithm:
1754 k ints/sec, 870 k doubles/sec, taus
1613 k ints/sec, 855 k doubles/sec, gfsr4
1370 k ints/sec, 769 k doubles/sec, mt19937
565 k ints/sec, 571 k doubles/sec, ranlxs0
400 k ints/sec, 405 k doubles/sec, ranlxs1
490 k ints/sec, 389 k doubles/sec, mrg
407 k ints/sec, 297 k doubles/sec, ranlux
243 k ints/sec, 254 k doubles/sec, ranlxd1
251 k ints/sec, 253 k doubles/sec, ranlxs2
238 k ints/sec, 215 k doubles/sec, cmrg
247 k ints/sec, 198 k doubles/sec, ranlux389
141 k ints/sec, 140 k doubles/sec, ranlxd2
Examples¶
The following program demonstrates the use of a random number generator to produce uniform random numbers in the range [0.0, 1.0),
#include <stdio.h>
#include <gsl/gsl_rng.h>
int
main (void)
{
const gsl_rng_type * T;
gsl_rng * r;
int i, n = 10;
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc (T);
for (i = 0; i < n; i++)
{
double u = gsl_rng_uniform (r);
printf ("%.5f\n", u);
}
gsl_rng_free (r);
return 0;
}
Here is the output of the program,
0.99974
0.16291
0.28262
0.94720
0.23166
0.48497
0.95748
0.74431
0.54004
0.73995
The numbers depend on the seed used by the generator. The default seed
can be changed with the GSL_RNG_SEED environment variable to
produce a different stream of numbers. The generator itself can be
changed using the environment variable GSL_RNG_TYPE. Here is the
output of the program using a seed value of 123 and the
multiple-recursive generator mrg:
$ GSL_RNG_SEED=123 GSL_RNG_TYPE=mrg ./a.out
0.33050
0.86631
0.32982
0.67620
0.53391
0.06457
0.16847
0.70229
0.04371
0.86374
References and Further Reading¶
The subject of random number generation and testing is reviewed extensively in Knuth’s Seminumerical Algorithms.
Donald E. Knuth, The Art of Computer Programming: Seminumerical Algorithms (Vol 2, 3rd Ed, 1997), Addison-Wesley, ISBN 0201896842.
Further information is available in the review paper written by Pierre L’Ecuyer,
P. L’Ecuyer, “Random Number Generation”, Chapter 4 of the Handbook on Simulation, Jerry Banks Ed., Wiley, 1998, 93–137.
http://www.iro.umontreal.ca/~lecuyer/papers.html in the file
handsim.ps.
The source code for the DIEHARD random number generator tests is also available online,
DIEHARD source code, G. Marsaglia, http://stat.fsu.edu/pub/diehard/
A comprehensive set of random number generator tests is available from NIST,
NIST Special Publication 800-22, “A Statistical Test Suite for the Validation of Random Number Generators and Pseudo Random Number Generators for Cryptographic Applications”.
Acknowledgements¶
Thanks to Makoto Matsumoto, Takuji Nishimura and Yoshiharu Kurita for making the source code to their generators (MT19937, MM&TN; TT800, MM&YK) available under the GNU General Public License. Thanks to Martin Luscher for providing notes and source code for the RANLXS and RANLXD generators.