Sorting¶
This chapter describes functions for sorting data, both directly and
indirectly (using an index). All the functions use the heapsort
algorithm. Heapsort is an 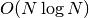 algorithm which operates
in-place and does not require any additional storage. It also provides
consistent performance, the running time for its worst-case (ordered
data) being not significantly longer than the average and best cases.
Note that the heapsort algorithm does not preserve the relative ordering
of equal elements—it is an unstable sort. However the resulting
order of equal elements will be consistent across different platforms
when using these functions.
algorithm which operates
in-place and does not require any additional storage. It also provides
consistent performance, the running time for its worst-case (ordered
data) being not significantly longer than the average and best cases.
Note that the heapsort algorithm does not preserve the relative ordering
of equal elements—it is an unstable sort. However the resulting
order of equal elements will be consistent across different platforms
when using these functions.
Sorting objects¶
The following function provides a simple alternative to the standard
library function qsort(). It is intended for systems lacking
qsort(), not as a replacement for it. The function qsort()
should be used whenever possible, as it will be faster and can provide
stable ordering of equal elements. Documentation for qsort() is
available in the GNU C Library Reference Manual.
The functions described in this section are defined in the header file
gsl_heapsort.h.
-
void gsl_heapsort(void *array, size_t count, size_t size, gsl_comparison_fn_t compare)¶
This function sorts the
countelements of the arrayarray, each of sizesize, into ascending order using the comparison functioncompare. The type of the comparison function is defined by-
type gsl_comparison_fn_t¶
int (*gsl_comparison_fn_t) (const void * a, const void * b)
A comparison function should return a negative integer if the first argument is less than the second argument,
0if the two arguments are equal and a positive integer if the first argument is greater than the second argument.For example, the following function can be used to sort doubles into ascending numerical order.
int compare_doubles (const double * a, const double * b) { if (*a > *b) return 1; else if (*a < *b) return -1; else return 0; }
The appropriate function call to perform the sort is:
gsl_heapsort (array, count, sizeof(double), compare_doubles);
Note that unlike
qsort()the heapsort algorithm cannot be made into a stable sort by pointer arithmetic. The trick of comparing pointers for equal elements in the comparison function does not work for the heapsort algorithm. The heapsort algorithm performs an internal rearrangement of the data which destroys its initial ordering.-
type gsl_comparison_fn_t¶
-
int gsl_heapsort_index(size_t *p, const void *array, size_t count, size_t size, gsl_comparison_fn_t compare)¶
This function indirectly sorts the
countelements of the arrayarray, each of sizesize, into ascending order using the comparison functioncompare. The resulting permutation is stored inp, an array of lengthn. The elements ofpgive the index of the array element which would have been stored in that position if the array had been sorted in place. The first element ofpgives the index of the least element inarray, and the last element ofpgives the index of the greatest element inarray. The array itself is not changed.
Sorting vectors¶
The following functions will sort the elements of an array or vector,
either directly or indirectly. They are defined for all real and integer
types using the normal suffix rules. For example, the float
versions of the array functions are gsl_sort_float() and
gsl_sort_float_index(). The corresponding vector functions are
gsl_sort_vector_float() and gsl_sort_vector_float_index(). The
prototypes are available in the header files gsl_sort_float.h
gsl_sort_vector_float.h. The complete set of prototypes can be
included using the header files gsl_sort.h and
gsl_sort_vector.h.
There are no functions for sorting complex arrays or vectors, since the ordering of complex numbers is not uniquely defined. To sort a complex vector by magnitude compute a real vector containing the magnitudes of the complex elements, and sort this vector indirectly. The resulting index gives the appropriate ordering of the original complex vector.
-
void gsl_sort(double *data, const size_t stride, size_t n)¶
This function sorts the
nelements of the arraydatawith stridestrideinto ascending numerical order.
-
void gsl_sort2(double *data1, const size_t stride1, double *data2, const size_t stride2, size_t n)¶
This function sorts the
nelements of the arraydata1with stridestride1into ascending numerical order, while making the same rearrangement of the arraydata2with stridestride2, also of sizen.
-
void gsl_sort_vector(gsl_vector *v)¶
This function sorts the elements of the vector
vinto ascending numerical order.
-
void gsl_sort_vector2(gsl_vector *v1, gsl_vector *v2)¶
This function sorts the elements of the vector
v1into ascending numerical order, while making the same rearrangement of the vectorv2.
-
void gsl_sort_index(size_t *p, const double *data, size_t stride, size_t n)¶
This function indirectly sorts the
nelements of the arraydatawith stridestrideinto ascending order, storing the resulting permutation inp. The arraypmust be allocated with a sufficient length to store thenelements of the permutation. The elements ofpgive the index of the array element which would have been stored in that position if the array had been sorted in place. The arraydatais not changed.
-
int gsl_sort_vector_index(gsl_permutation *p, const gsl_vector *v)¶
This function indirectly sorts the elements of the vector
vinto ascending order, storing the resulting permutation inp. The elements ofpgive the index of the vector element which would have been stored in that position if the vector had been sorted in place. The first element ofpgives the index of the least element inv, and the last element ofpgives the index of the greatest element inv. The vectorvis not changed.
Selecting the k smallest or largest elements¶
The functions described in this section select the 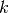 smallest
or largest elements of a data set of size
smallest
or largest elements of a data set of size 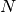 . The routines use an
. The routines use an
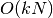 direct insertion algorithm which is suited to subsets that
are small compared with the total size of the dataset. For example, the
routines are useful for selecting the 10 largest values from one million
data points, but not for selecting the largest 100,000 values. If the
subset is a significant part of the total dataset it may be faster
to sort all the elements of the dataset directly with an
direct insertion algorithm which is suited to subsets that
are small compared with the total size of the dataset. For example, the
routines are useful for selecting the 10 largest values from one million
data points, but not for selecting the largest 100,000 values. If the
subset is a significant part of the total dataset it may be faster
to sort all the elements of the dataset directly with an 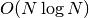 algorithm and obtain the smallest or largest values that way.
algorithm and obtain the smallest or largest values that way.
-
int gsl_sort_smallest(double *dest, size_t k, const double *src, size_t stride, size_t n)¶
This function copies the
ksmallest elements of the arraysrc, of sizenand stridestride, in ascending numerical order into the arraydest. The sizekof the subset must be less than or equal ton. The datasrcis not modified by this operation.
-
int gsl_sort_largest(double *dest, size_t k, const double *src, size_t stride, size_t n)¶
This function copies the
klargest elements of the arraysrc, of sizenand stridestride, in descending numerical order into the arraydest.kmust be less than or equal ton. The datasrcis not modified by this operation.
-
int gsl_sort_vector_smallest(double *dest, size_t k, const gsl_vector *v)¶
-
int gsl_sort_vector_largest(double *dest, size_t k, const gsl_vector *v)¶
These functions copy the
ksmallest or largest elements of the vectorvinto the arraydest.kmust be less than or equal to the length of the vectorv.
The following functions find the indices of the 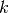 smallest or
largest elements of a dataset.
smallest or
largest elements of a dataset.
-
int gsl_sort_smallest_index(size_t *p, size_t k, const double *src, size_t stride, size_t n)¶
This function stores the indices of the
ksmallest elements of the arraysrc, of sizenand stridestride, in the arrayp. The indices are chosen so that the corresponding data is in ascending numerical order.kmust be less than or equal ton. The datasrcis not modified by this operation.
-
int gsl_sort_largest_index(size_t *p, size_t k, const double *src, size_t stride, size_t n)¶
This function stores the indices of the
klargest elements of the arraysrc, of sizenand stridestride, in the arrayp. The indices are chosen so that the corresponding data is in descending numerical order.kmust be less than or equal ton. The datasrcis not modified by this operation.
-
int gsl_sort_vector_smallest_index(size_t *p, size_t k, const gsl_vector *v)¶
-
int gsl_sort_vector_largest_index(size_t *p, size_t k, const gsl_vector *v)¶
These functions store the indices of the
ksmallest or largest elements of the vectorvin the arrayp.kmust be less than or equal to the length of the vectorv.
Computing the rank¶
The rank of an element is its order in the sorted data. The rank
is the inverse of the index permutation, 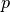 . It can be computed
using the following algorithm:
. It can be computed
using the following algorithm:
for (i = 0; i < p->size; i++)
{
size_t pi = p->data[i];
rank->data[pi] = i;
}
This can be computed directly from the function
gsl_permutation_inverse(rank,p).
The following function will print the rank of each element of the vector
 :
:
void
print_rank (gsl_vector * v)
{
size_t i;
size_t n = v->size;
gsl_permutation * perm = gsl_permutation_alloc(n);
gsl_permutation * rank = gsl_permutation_alloc(n);
gsl_sort_vector_index (perm, v);
gsl_permutation_inverse (rank, perm);
for (i = 0; i < n; i++)
{
double vi = gsl_vector_get(v, i);
printf ("element = %d, value = %g, rank = %d\n",
i, vi, rank->data[i]);
}
gsl_permutation_free (perm);
gsl_permutation_free (rank);
}
Examples¶
The following example shows how to use the permutation 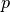 to print
the elements of the vector
to print
the elements of the vector  in ascending order:
in ascending order:
gsl_sort_vector_index (p, v);
for (i = 0; i < v->size; i++)
{
double vpi = gsl_vector_get (v, p->data[i]);
printf ("order = %d, value = %g\n", i, vpi);
}
The next example uses the function gsl_sort_smallest() to select
the 5 smallest numbers from 100000 uniform random variates stored in an
array,
#include <gsl/gsl_rng.h>
#include <gsl/gsl_sort_double.h>
int
main (void)
{
const gsl_rng_type * T;
gsl_rng * r;
size_t i, k = 5, N = 100000;
double * x = malloc (N * sizeof(double));
double * small = malloc (k * sizeof(double));
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc (T);
for (i = 0; i < N; i++)
{
x[i] = gsl_rng_uniform(r);
}
gsl_sort_smallest (small, k, x, 1, N);
printf ("%zu smallest values from %zu\n", k, N);
for (i = 0; i < k; i++)
{
printf ("%zu: %.18f\n", i, small[i]);
}
free (x);
free (small);
gsl_rng_free (r);
return 0;
}
The output lists the 5 smallest values, in ascending order,
5 smallest values from 100000
0: 0.000003489200025797
1: 0.000008199829608202
2: 0.000008953968062997
3: 0.000010712770745158
4: 0.000033531803637743
References and Further Reading¶
The subject of sorting is covered extensively in the following,
Donald E. Knuth, The Art of Computer Programming: Sorting and Searching (Vol 3, 3rd Ed, 1997), Addison-Wesley, ISBN 0201896850.
The Heapsort algorithm is described in the following book,
Robert Sedgewick, Algorithms in C, Addison-Wesley, ISBN 0201514257.