29.1 One-dimensional Interpolation ¶
Octave supports several methods for one-dimensional interpolation, most of which are described in this section. Polynomial Interpolation and Interpolation on Scattered Data describe additional methods.
- :
yi =interp1(x, y, xi)¶ - :
yi =interp1(y, xi)¶ - :
yi =interp1(…, method)¶ - :
yi =interp1(…, extrap)¶ - :
yi =interp1(…, "left")¶ - :
yi =interp1(…, "right")¶ - :
pp =interp1(…, "pp")¶ -
One-dimensional interpolation.
Interpolate input data to determine the value of yi at the points xi. If not specified, x is taken to be the indices of y (
1:length (y)). If y is a matrix or an N-dimensional array, the interpolation is performed on each column of y.The interpolation method is one of:
"nearest"Return the nearest neighbor.
"previous"Return the previous neighbor.
"next"Return the next neighbor.
"linear"(default)Linear interpolation from nearest neighbors.
"pchip"Piecewise cubic Hermite interpolating polynomial—shape-preserving interpolation with smooth first derivative.
"cubic"Cubic interpolation (same as
"pchip")."spline"Cubic spline interpolation—smooth first and second derivatives throughout the curve.
Adding ’*’ to the start of any method above forces
interp1to assume that x is uniformly spaced, and onlyx(1)andx(2)are referenced. This is usually faster, and is never slower. The default method is"linear".If extrap is the string
"extrap", then extrapolate values beyond the endpoints using the current method. If extrap is a number, then replace values beyond the endpoints with that number. When unspecified, extrap defaults toNA.If the string argument
"pp"is specified, then xi should not be supplied andinterp1returns a piecewise polynomial object. This object can later be used withppvalto evaluate the interpolation. There is an equivalence, such thatppval (interp1 (x, y, method,."pp"), xi) == interp1 (x, y, xi, method,"extrap")Duplicate points in x specify a discontinuous interpolant. There may be at most 2 consecutive points with the same value. If x is increasing, the default discontinuous interpolant is right-continuous. If x is decreasing, the default discontinuous interpolant is left-continuous. The continuity condition of the interpolant may be specified by using the options
"left"or"right"to select a left-continuous or right-continuous interpolant, respectively. Discontinuous interpolation is only allowed for"nearest"and"linear"methods; in all other cases, the x-values must be unique.An example of the use of
interp1isxf = [0:0.05:10]; yf = sin (2*pi*xf/5); xp = [0:10]; yp = sin (2*pi*xp/5); lin = interp1 (xp, yp, xf); near = interp1 (xp, yp, xf, "nearest"); pch = interp1 (xp, yp, xf, "pchip"); spl = interp1 (xp, yp, xf, "spline"); plot (xf,yf,"r", xf,near,"g", xf,lin,"b", xf,pch,"c", xf,spl,"m", xp,yp,"r*"); legend ("original", "nearest", "linear", "pchip", "spline");See also: pchip, spline, interpft, interp2, interp3, interpn.
There are some important differences between the various interpolation
methods. The "spline" method enforces that both the first and second
derivatives of the interpolated values have a continuous derivative,
whereas the other methods do not. This means that the results of the
"spline" method are generally smoother. If the function to be
interpolated is in fact smooth, then "spline" will give excellent
results. However, if the function to be evaluated is in some manner
discontinuous, then "pchip" interpolation might give better results.
This can be demonstrated by the code
t = -2:2;
dt = 1;
ti =-2:0.025:2;
dti = 0.025;
y = sign (t);
ys = interp1 (t,y,ti,"spline");
yp = interp1 (t,y,ti,"pchip");
ddys = diff (diff (ys)./dti) ./ dti;
ddyp = diff (diff (yp)./dti) ./ dti;
figure (1);
plot (ti,ys,"r-", ti,yp,"g-");
legend ("spline", "pchip", 4);
figure (2);
plot (ti,ddys,"r+", ti,ddyp,"g*");
legend ("spline", "pchip");
The result of which can be seen in Figure 29.1 and Figure 29.2.
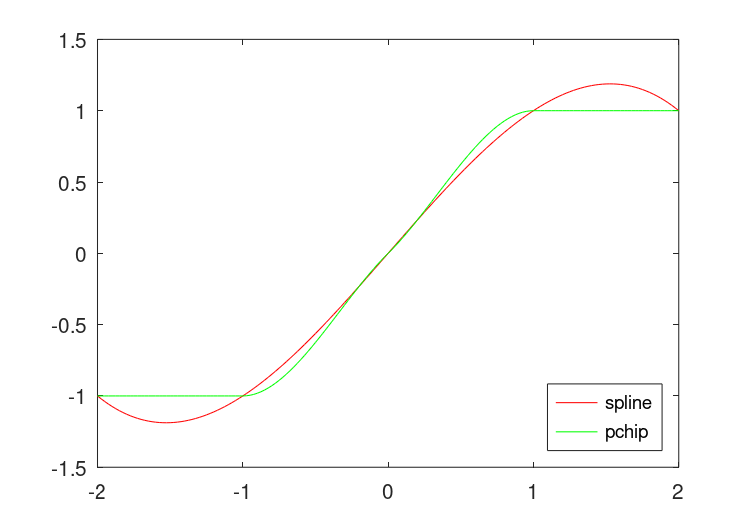
Figure 29.1: Comparison of "pchip" and "spline" interpolation methods for a
step function
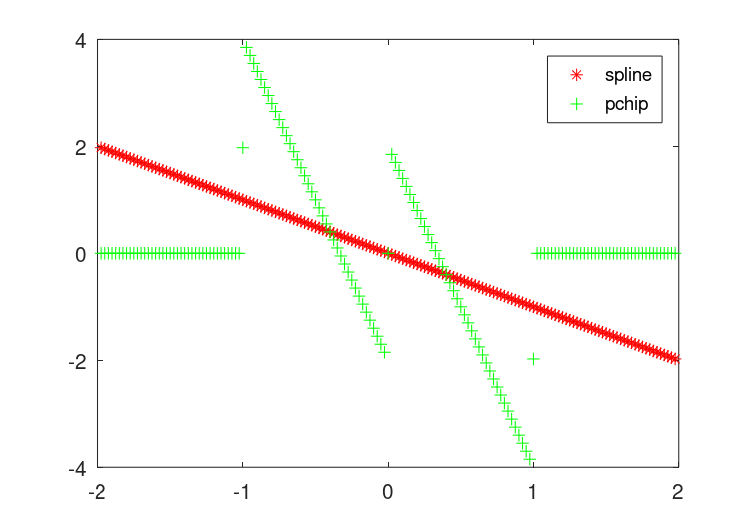
Figure 29.2: Comparison of the second derivative of the "pchip" and "spline"
interpolation methods for a step function
Fourier interpolation, is a resampling technique where a signal is converted to the frequency domain, padded with zeros and then reconverted to the time domain.
- :
y =interpft(x, n)¶ - :
y =interpft(x, n, dim)¶ -
Fourier interpolation.
If x is a vector then x is resampled with n points. The data in x is assumed to be equispaced. If x is a matrix or an N-dimensional array, the interpolation is performed on each column of x.
If dim is specified, then interpolate along the dimension dim.
interpftassumes that the interpolated function is periodic, and so assumptions are made about the endpoints of the interpolation.See also: interp1.
There are two significant limitations on Fourier interpolation. First,
the function signal is assumed to be periodic, and so non-periodic
signals will be poorly represented at the edges. Second, both the
signal and its interpolation are required to be sampled at equispaced
points. An example of the use of interpft is
t = 0 : 0.3 : pi; dt = t(2)-t(1);
n = length (t); k = 100;
ti = t(1) + [0 : k-1]*dt*n/k;
y = sin (4*t + 0.3) .* cos (3*t - 0.1);
yp = sin (4*ti + 0.3) .* cos (3*ti - 0.1);
plot (ti, yp, "g", ti, interp1 (t, y, ti, "spline"), "b", ...
ti, interpft (y, k), "c", t, y, "r+");
legend ("sin(4t+0.3)cos(3t-0.1)", "spline", "interpft", "data");
which demonstrates the poor behavior of Fourier interpolation for non-periodic functions, as can be seen in Figure 29.3.
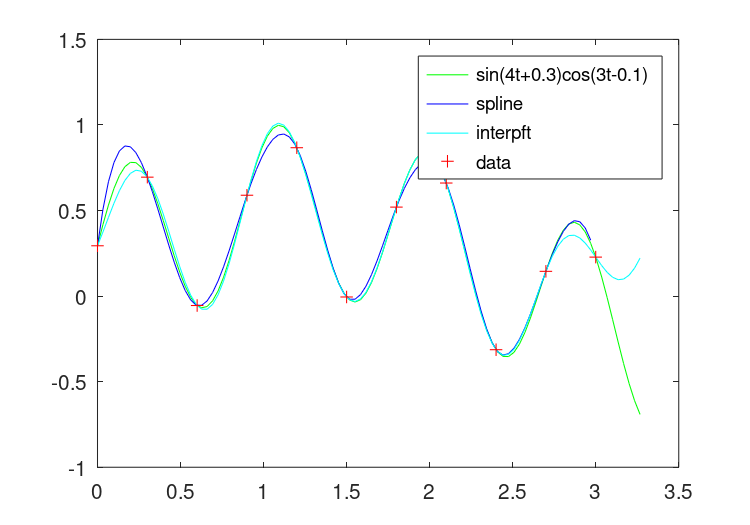
Figure 29.3: Comparison of interp1 and interpft for non-periodic data
In addition, the support functions spline and lookup that
underlie the interp1 function can be called directly.
- :
pp =spline(x, y)¶ - :
yi =spline(x, y, xi)¶ Return the cubic spline interpolant of points x and y.
When called with two arguments, return the piecewise polynomial pp that may be used with
ppvalto evaluate the polynomial at specific points.When called with a third input argument,
splineevaluates the spline at the points xi. The third calling formspline (x, y, xi)is equivalent toppval (spline (x, y), xi).The variable x must be a vector of length n.
y can be either a vector or array. If y is a vector it must have a length of either n or
n + 2. If the length of y is n, then the"not-a-knot"end condition is used. If the length of y isn + 2, then the first and last values of the vector y are the values of the first derivative of the cubic spline at the endpoints.If y is an array, then the size of y must have the form
[s1, s2, …, sk, n]or[s1, s2, …, sk, n + 2]. The array is reshaped internally to a matrix where the leading dimension is given bys1 * s2 * … * skand each row of this matrix is then treated separately. Note that this is exactly the opposite ofinterp1but is done for MATLAB compatibility.