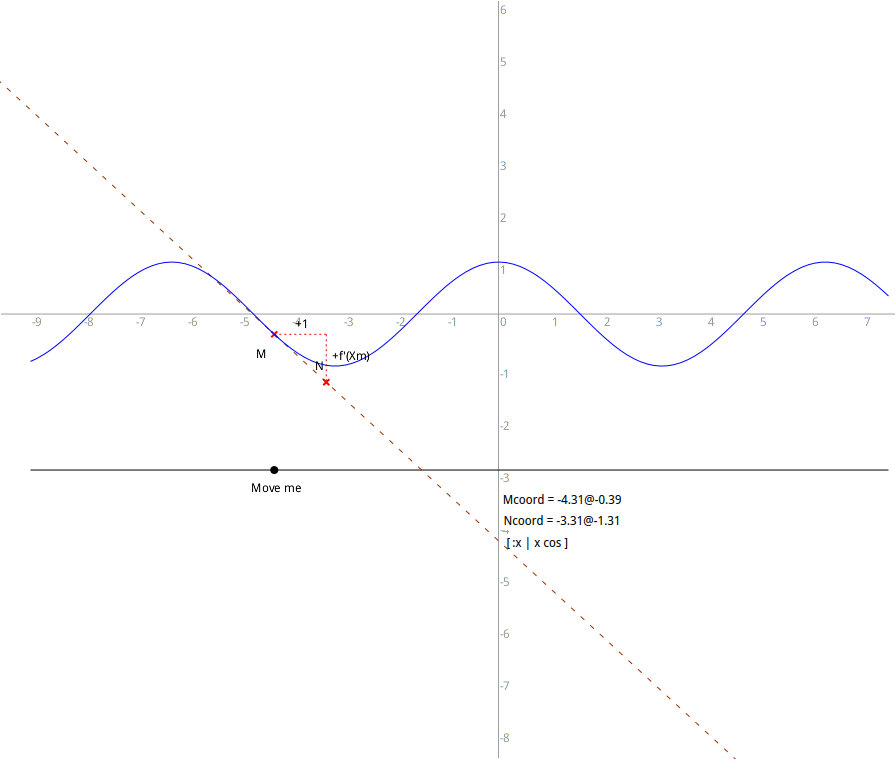
Figure 6.5: Courbe et tangente en un point
Next: Éditer un script comme un pro, Previous: Script avec deux paramètres, Up: Script Pharo [Index]
Dans la section suivante, nous présentons une figure plus complexe intégrant un enchaînement de scripts pour la construction d’une portion de courbe représentative d’une fonction et la tangente en un point mobile de cette portion de courbe.
La figure finale est disponible dans le dossier examples de Dr.Geo, elle s’appelle Curve and slope.fgeo.
Dans une nouvelle figure, nous commençons par construire un segment horizontal, nous y plaçons un point libre appelé “Move me”. Ce point servira de base à la construction de la courbe comme lieu d’un point.
Comme un script est capable de retourner n’importe quel type d’objet,
le premier de notre construction définira simplement la fonction
utilisée. Pour ce faire nous utilisons des objets Pharo de type
bloc de code – fonction anonyme en Lisp. Nous nommons ce script
Function, sans arguments, sa méthode compute est :
compute "La définition de notre fonction" ^ [:x | x cos]
Ensuite nous le plaçons dans la figure18. Ainsi le bloc de code retourné par Function attend un argument :x et retourne le cosinus de celui-ci. Nous verrons dans la suite comment manipuler ce script.
Maintenant nous calculons les coordonnées d’un point appartenant à la courbe. Nous utilisons notre point “Move me” et notre fonction. Ce script Mcoord aura comme arguments ce point et le script Function (dans cet ordre) :
compute ^ (self arg1 x) @ (self arg2 compute value: self arg1 x)
L’abscisse de ses coordonnées est la même que celle du point de départ, son ordonnée est l’image de son abscisse par la fonction.
Noter :
self arg2, l’accès au script Function, qui est un
bloc de code définissant la fonction ;
Maintenant utilisons ce script Mcoord avec comme argument le point “Move me!” ; le résultat du script est de la forme 1.2@0.5, cela représente un couple de coordonnées.
Avec l’outil point ...Points → Coordonnées... créons un point ayant ses coordonnées contraintes par le résultat de ce script.
L’outil lieu d’un point ...Lignes → Lieu de point... donne ensuite la courbe en sélectionnant nos deux points.
Pour ce faire, nous calculons une valeur approchée de la pente en un point de la courbe, avec celle-ci nous déduirons un deuxième point de la tangente.
p = ( f(x + 0.0001) - f(x) ) / 0.0001
Cela se traduit par un script Ncoord avec comment argument le point où calculer une approximation de la pente et le script Function :
compute | p x f | f := self arg2 compute. x := self arg1 point x. p := ((f value: x + 0.0001) - (f value: x)) / 0.0001. ^ self arg1 point + (1 @ p)
Nous plaçons ensuite ce script dans la figure.
Noter :
Utilisons ce script avec comme arguments le point de notre courbe et notre script Function. Nous obtenons un deuxième couple de coordonnées. Avec celles-ci construisons un point, la tangente est la droite définie par ce point et celui de la courbe.
En déplaçant le point “Move me!”, la tangente est recalculée. Tout aussi intéressant : modifier le script Function actualise correctement l’ensemble de notre construction. Quelques exemples de modifications :
^ [:x | x * x / 10] ^ [:x | x cos + (10 * x) sin] ^ [:x | (x * 5) cos + x abs]
Il est important de le référencer dans la figure afin qu’il soit inclus dans la description de celle-ci lors d’une opération de sauvegarde sur fichier.
Next: Éditer un script comme un pro, Previous: Script avec deux paramètres, Up: Script Pharo [Index]