9.12 Example 12

In the structure of the image all the joints are pin joints. Ignoring the weight of the beams, get all the reactions in the joints.

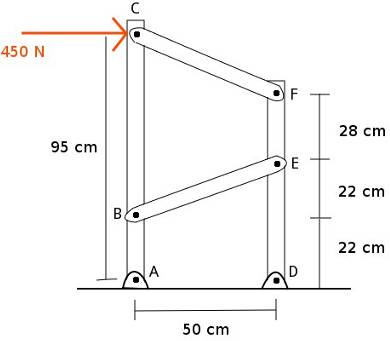
Solution with FisicaLab

Notice that the beams BE and CF are beams of two forces. So, we build the problem with two elements Beam, and the necessary elements Force and Beams of 2 forces, as show below:

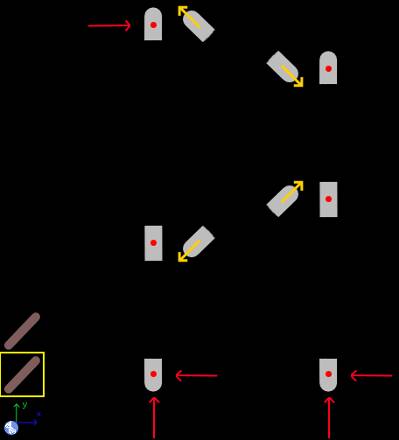
The Stationary reference system set the gravity value to default. Now to the element Beam that represent the ABC beam, we have:

Name

ABC

m

0

lc

0

ang

90

This beam have three elements: A, B and C. To the element that correspond with A:

Name

ABC

l

0

And to the applied Forces, the reactions:

f

RAx

f

RAy

Now to the element that correspond with B:

Name

ABC

l

22 @ cm

And to the element Beam of 2 forces, that correspond with the beam from B to E, the angle is entered as the slope 22/50:

f

BE

ang

23.749

To the element that correspond with C:

Name

ABC

l

95 @ cm

To the element Force, that correspond with the force of 450 N:

f

450

And to the element Beam of 2 forces, that correspond with the beam from C to F, the angle is entered as the slope 23/50:

f

CF

ang

24.702

Now to the element Beam that represent the DEF beam, we have:

Name

DEF

m

0

lc

0

ang

90

This beam have three elements: D, E and F. To the element that correspond with D:

Name

DEF

l

0

And to the applied Forces, the reactions:

f

RDy

f

RDx

To the element that correspond with E:

Name

DEF

l

44 @ cm

And to the element Beam of 2 forces, that correspond with the beam from B to E, the angle is also the slope 22/50:

f

BE

ang

23.749

To the element that correspond with F:

Name

DEF

l

72 @ cm

And to the element Beam of 2 forces, that correspond with the beam from C to F, the angle is also the slope 23/50:

f

CF

ang

24.702

Now click in the icon Solve to get the answer:

RDy = 854.981 N ;  RDx = -461.094 N ;
BE = -1295.364 N [tension] ;
CF = 797.558 N [compression] ;  RAy = -854.981 N ;
RAx = 911.094 N ;
Status = success.