13.13 Example 13

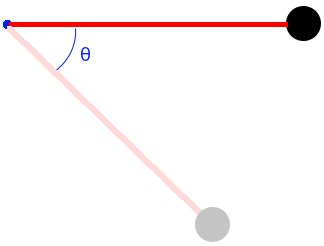
A small sphere of ​​400 grams, tied to a rope of 60 cm, can oscillate in a vertical plane. If the sphere is released from rest when the rope is stretched horizontally. And if the maximum tension that this support is 7 N, find the angle when the rope breaks.

Solution with FisicaLab

Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add one element Stationary reference system, one element Object in rest, one element Mobile with circular movement, one element Force, one element Energy and one element Sine of angle. As show the image below:

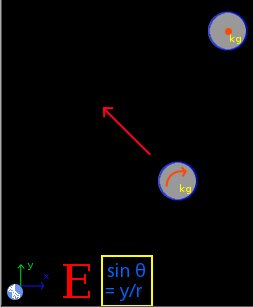
The element Stationary reference system write to default the gravity value. And the time is irrelevant for this problem. Now the element Object in rest represents the initial state. If we take as horizontal reference this position, we have for this element:

Name

A

m

400 @ g

y

0

To the element Mobile with circular movement, which represents the final state, and taking into account that both the speed and height are unknowns, we have:

Name

B

m

400 @ g

vt

vt

r

60 @ cm

y

yB

And to the Force element, which represents the force applied by the rope and taking into account that the angle of the force is the same as that of the rope, we have:

f

7

ang

ang

Now for the Sine of angle element, where we relate the height of the sphere in the final state and the turning radius with the unknown angle, we have:

y

yB

r

60 @ cm

ang

ang

Finally for the element Energy, and knowing that energy is conserved, we have:

System i

A

System f

B

W

0

Now click in the icon Solve to get the answer:

yB = -0.357 m ;  ang = 36.486 degrees ;  vt = 2.646 m/s ;
Status = success.