Next: Example 3, Previous: Example 1, Up: Examples circular dynamics of particles [Contents][Index]
13.2 Example 2
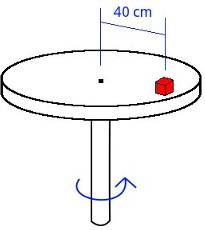
A small block A is on a table that rotates from rest with a constant tangential acceleration. If the coefficient of static friction between the block and the turntable is 0.57, find the minimum interval of time for the block to reach a speed of 1.2 m/s without slip.
Solution with FisicaLab
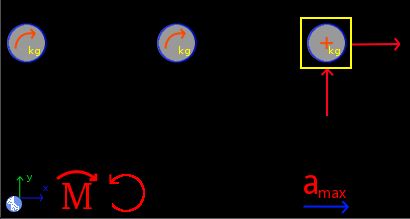
Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add one element Stationary reference system, two elements Mobile with circular movement, one element Mobile with perpendicular circular movement, two element Force, one element Angular momentum, one element Moment of a force and one element Maximum acceleration. As show the image below:
The element Stationary reference system write to default the gravity value. And the time is unknown.
- g
9.81
- t
time
The mass of the block is not provided, since it is irrelevant to what is asked. But as we need to specify a mass, will place 1 kg. Thus, for the element Mobile with circular movement placed at left, which represents the initial state, we have:
- Name
initial
- m
1
- vt
0
- r
40 @ cm
- y
0
For the another element Mobile with circular movement, placed at right, which represents the final state, we have:
- Name
final
- m
1
- vt
1.2
- r
40 @ cm
- y
0
Now we add both objects to element Angular momentum, where M is the moment that causes the acceleration of the block:
- System i
initial
- System f
final
- M
M
The element Mobile with perpendicular circular motion is used to set additional conditions on the final state. Calling it A and leaving the center of rotation to the right, we have (both, the tangential acceleration and the tangential force, are unknowns):
- Name
A
- m
1
- vt
1.2
- r
40 @ cm
- at
at
- Ft
Ft
- C
>
And in the element Maximum acceleration, we add the coefficient of friction, which ensures that both, the tangential force (Ft) and the centripetal force, are due to the maximum friction force:
- Object
A
- u
0.57
Now the element Moment of a force, is used to relate the maximum tangential force (Ft) with the applied moment:
- M
M
- f
Ft
- d
40 @ cm
Finally, for normal and centripetal forces we have, respectively:
- f
normal
- f
centripetal
Now click in the icon Solve to get the answer:
centripetal = 3.600 N ; time = 0.280 s ; M = 1.711 N*m ; at = 4.279 m/s2 ; Ft = 4.279 N ; normal = 9.810 N ; Status = success.
The minimum time is 0.28 seconds.