13.6 Example 6

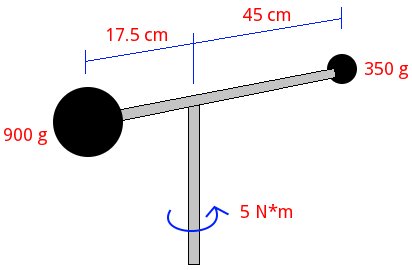
A system consisting of two small spheres of 900 and 350 grams, joined by a thin rod can rotate freely about a vertical axis passing through the center of mass of the system. Initially the system is at rest when a moment of 5 N*m is applied. Neglecting the mass of the rod, find the angular velocity and angular acceleration of the system after 1.2 seconds. Find also the power applied.

Solution with FisicaLab

Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add one element Stationary reference system, four elements Mobile with circular movement, one element Mobile with perpendicular circular movement, two elements Force, one element Initial system, one element Final system, one element Power, one element Angular momentum, two elements Angular velocity, one element Angular acceleration, one element Moment of a force and one element Inertia. As show the image below:

The element Stationary reference system write to default the gravity value. And the time is 1.2 seconds:

g

9.81

t

1.2

The two elements Mobile with circular movement at top represents the initial state of the system. Taking the left as the sphere of 900 grams, which we call Ainitial, and the right as the sphere of 350 grams, which we call Binitial, we have respectively:

Name

Ainitial

m

900 @ g

vt

0

r

17.5 @ cm

y

0

Name

Binitial

m

350 @ g

vt

0

r

45 @ cm

y

0

Now we add these to the Initial system element, which we call initial:

Name

initial

Object 1

Ainitial

Object 2

Binitial

Object 3

0

Object 4

0

The two elements Mobile with circular movement on the bottom represents the final state. Calling Afinal the sphere of 900 grams and Bfinal the sphere of 350 grams, we have:

Name

Afinal

m

900 @ g

vt

vtAfinal

r

17.5 @ cm

y

0

Name

Bfinal

m

350 @ g

vt

vtBfinal

r

45 @ cm

y

0

Now we add these to the Final system element, which we call final:

Name

final

Object 1

Afinal

Object 2

Bfinal

Object 3

0

Object 4

0

Now add the two systems to element Angular momentum, where we put also the applied momentum:

System i

initial

System f

final

M

5

Also add these to the Power element, where we put the power as an unknown:

System i

initial

System f

final

P

power

Now in Angular velocity elements, put the final angular velocity as an unknown (the same for both spheres):

Object

Afinal

vang

vang

Object

Bfinal

vang

vang

We use the element Mobile with perpendicular circular movement to know the angular acceleration, applying the force produced by the applied moment. But since the system have two spheres with different mass and different radius, first we get the total mass and the effective turning radius of the final system, using the Inertia element:

System

final

m

mTotal

r

radius

Now we can obtain the corresponding force for this system using the element Moment of a force:

M

5

f

Ft

d

radius

Now enter these information in the element Mobile with perpendicular circular movement, which we call system. As tangential velocity for this system we will place 0, the initial velocity (Since the angular acceleration is constant, has the same value at initial or final state. Anyway, we don’t know the final velocity of this mobile.):

Name

system

m

mTotal

vt

0

r

radius

at

at

Ft

Ft

C

>

And to the applied forces:

f

normal

f

centripetal

Finally in the Angular acceleration element, we assign the Mobile with perpendicular circular movement:

Object

system

aang

aang

Now click in the icon Solve to get the answer:

normal = 12.263 N ;  centripetal = -0.000 N ;
mTotal = 1.250 kg ;  radius = 0.281 m ;
Ft = 17.817 N ;  aang = 50.794 rad/s2 ;
vtAfinal = 10.667 m/s ;  vtBfinal = 27.429 m/s ;
vang = 60.952 rad/s ;  power = 152.381 N*m/s ;
at = 14.254 m/s2 ;
Status = success.