13.8 Example 8

A small disc of 500 grams and another of 1.5 kg are tied by a rope of 48 cm. Both disks rotate in the direction of clockwise with an angular velocity of 8 rad/s around the center of mass. At the time shown in the image, the center of mass intersects the X axis at 2 meters from the origin with an speed of 0.45 m/s at 55 degrees from the horizontal. Moments after the rope breaks, and it is observed that the disk of 1.5 kg is moved parallel to the axis X and the disk of 500 grams intersects the Y axis at a distance of 4.6 m from the origin. Find a) The speed of both discs after the rope breaks and b) the distance d between the X axis and the trajectory of the disk of 1.5 kg.

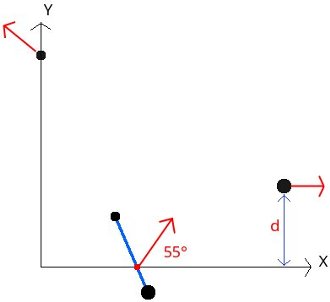
Solution with FisicaLab

Select the Dynamics group and, inside this, the Circular module. Erase the content of the chalkboard and select the SI system. And add two elements Mobile with circular movement, two elements Mobile with linear movement, one element Center of rotation, one element Initial system, one element Final system, two elements Angular velocity, one element Energy, one element Angular momentum and one element Linear momentum. As show the image below:

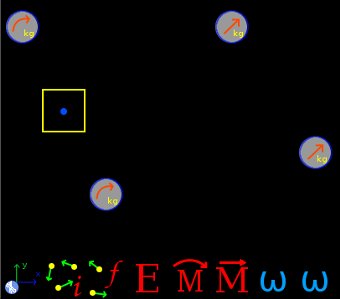
The two elements Mobile with circular movement at left represent the initial state of the system. Taking the left as the disk of 500 grams, which we call Ainitial, and the right as the disk of 1.5 kg, which we call Binitial, we have respectively (the distance from each disk to the center of rotation can be obtained using the rd() function and applying the conversion factor):

Name

Ainitial

m

500 @ g

vt

vtA

r

36 @ cm

y

0

Name

Binitial

m

1.5

vt

vtB

r

12 @ cm

y

0

The tangential velocity is unknown. But we know the angular velocity. Therefore to Angular velocity elements, remember that rotation is in sense of clockwise:

Object

Ainitial

vang

-8

Object

Binitial

vang

-8

Now for the element Center of rotation, which also forms part of the initial state:

Name

center

v

0.45

ang

55

x

2

y

0

As the two elements Mobile with circular movement and Center of rotation are the initial state, we add them to the element Initial system, which we call initial:

Name

initial

Object 1

centtr

Object 2

Ainitial

Object 3

Binitial

Object 4

0

Now for the element Mobile with linear movement at top, that represent the disk of 500 grams that intersect the axis Y, we have, calling it Afinal:

Name

Afinal

m

500 @ g

v

vAfinal

x

0

y

4.6

ang

angA

a

0

For the other element Mobile with linear movement at bottom, which represents the disk of 1.5 kg which travels parallel to the X axis at a distance d, and calling it Bfinal:

Name

Bfinal

m

1.5

v

vBfinal

x

0

y

d

ang

0

a

0

These two elements form the final state, then we add them to the element Final system, which we call final:

Name

final

Object 1

Afinal

Object 2

Bfinal

Object 3

0

Object 4

0

Now for the element Energy, knowing that energy is conserved, we have:

System i

initial

System f

final

W

0

To the element Angular momentum, taking into account that no external moments applied:

System i

initial

System f

final

M

0

And to element Linear momentum, no external forces are applied, we have:

System i

initial

System f

final

Fx

0

Fy

0

Now click in the icon Solve to get the answer:

vBfinal = 1.145 m/s ;  d = 2.761 m ;  vtA = -2.880 m/s ;
vtB = -0.960 m/s ;  vAfinal = 2.818 m/s ;
angA = 148.447 degrees ;
Status = success.