9.1.1 Distance on a 2D curved space ¶
The observations to date (for example, the Planck 2015 results), have not measured232 the presence of significant curvature in the universe. However to be generic (and allow its measurement if it does in fact exist), it is very important to create a framework that allows non-zero uniform curvature. However, this section is not intended to be a fully thorough and mathematically complete derivation of these concepts. There are many references available for such reviews that go deep into the abstract mathematical proofs. The emphasis here is on visualization of the concepts for a beginner.
As 3D beings, it is difficult for us to mentally create (visualize) a picture of the curvature of a 3D volume. Hence, here we will assume a 2D surface/space and discuss distances on that 2D surface when it is flat and when it is curved. Once the concepts have been created/visualized here, we will extend them, in Extending distance concepts to 3D, to a real 3D spatial slice of the Universe we live in and hope to study.
To be more understandable (actively discuss from an observer’s point of view) let’s assume there’s an imaginary 2D creature living on the 2D space (which might be curved in 3D). Here, we will be working with this creature in its efforts to analyze distances in its 2D universe. The start of the analysis might seem too mundane, but since it is difficult to imagine a 3D curved space, it is important to review all the very basic concepts thoroughly for an easy transition to a universe that is more difficult to visualize (a curved 3D space embedded in 4D).
To start, let’s assume a static (not expanding or shrinking), flat 2D surface similar to Figure 9.1 and that the 2D creature is observing its universe from point \(A\). One of the most basic ways to parameterize this space is through the Cartesian coordinates (\(x\), \(y\)). In Figure 9.1, the basic axes of these two coordinates are plotted. An infinitesimal change in the direction of each axis is written as \(dx\) and \(dy\). For each point, the infinitesimal changes are parallel with the respective axes and are not shown for clarity. Another very useful way of parameterizing this space is through polar coordinates. For each point, we define a radius (\(r\)) and angle (\(\phi\)) from a fixed (but arbitrary) reference axis. In Figure 9.1 the infinitesimal changes for each polar coordinate are plotted for a random point and a dashed circle is shown for all points with the same radius.
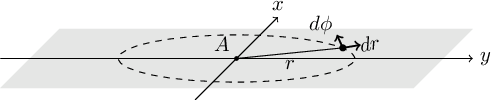
Figure 9.1: Two dimensional Cartesian and polar coordinates on a flat plane.
Assuming an object is placed at a certain position, which can be parameterized as \((x,y)\), or \((r,\phi)\), a general infinitesimal change in its position will place it in the coordinates \((x+dx,y+dy)\), or \((r+dr,\phi+d\phi)\). The distance (on the flat 2D surface) that is covered by this infinitesimal change in the static universe (\(ds_s\), the subscript signifies the static nature of this universe) can be written as:
$$ds_s^2=dx^2+dy^2=dr^2+r^2d\phi^2$$
The main question is this: how can the 2D creature incorporate the (possible) curvature in its universe when it’s calculating distances? The universe that it lives in might equally be a curved surface like Figure 9.2. The answer to this question but for a 3D being (us) is the whole purpose to this discussion. Here, we want to give the 2D creature (and later, ourselves) the tools to measure distances if the space (that hosts the objects) is curved.
Figure 9.2 assumes a spherical shell with radius \(R\) as the curved 2D plane for simplicity. The 2D plane is tangent to the spherical shell and only touches it at \(A\). This idea will be generalized later. The first step in measuring the distance in a curved space is to imagine a third dimension along the \(z\) axis as shown in Figure 9.2. For simplicity, the \(z\) axis is assumed to pass through the center of the spherical shell. Our imaginary 2D creature cannot visualize the third dimension or a curved 2D surface within it, so the remainder of this discussion is purely abstract for it (similar to us having difficulty in visualizing a 3D curved space in 4D). But since we are 3D creatures, we have the advantage of visualizing the following steps. Fortunately the 2D creature is already familiar with our mathematical constructs, so it can follow our reasoning.
With the third axis added, a generic infinitesimal change over the full 3D space corresponds to the distance:
$$ds_s^2=dx^2+dy^2+dz^2=dr^2+r^2d\phi^2+dz^2.$$
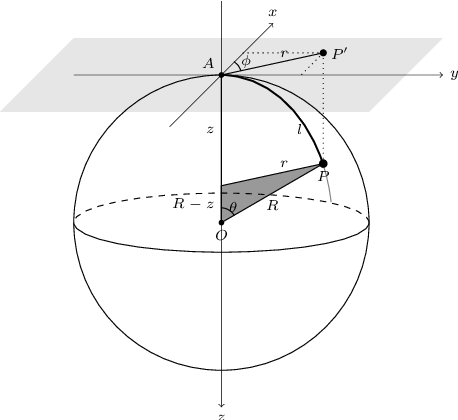
Figure 9.2: 2D spherical shell (centered on \(O\)) and flat plane (light gray) tangent to it at point \(A\).
It is very important to recognize that this change of distance is for any point in the 3D space, not just those changes that occur on the 2D spherical shell of Figure 9.2. Recall that our 2D friend can only do measurements on the 2D surfaces, not the full 3D space. So we have to constrain this general change to any change on the 2D spherical shell. To do that, let’s look at the arbitrary point \(P\) on the 2D spherical shell. Its image (\(P'\)) on the flat plain is also displayed. From the dark gray triangle, we see that
$$\sin\theta={r\over R},\quad\cos\theta={R-z\over R}.$$These relations allow the 2D creature to find the value of \(z\) (an abstract dimension for it) as a function of r (distance on a flat 2D plane, which it can visualize) and thus eliminate \(z\). From \(\sin^2\theta+\cos^2\theta=1\), we get \(z^2-2Rz+r^2=0\) and solving for \(z\), we find:
$$z=R\left(1\pm\sqrt{1-{r^2\over R^2}}\right).$$
The \(\pm\) can be understood from Figure 9.2: For each \(r\), there are two points on the sphere, one in the upper hemisphere and one in the lower hemisphere. An infinitesimal change in \(r\), will create the following infinitesimal change in \(z\):
$$dz={\mp r\over R}\left(1\over \sqrt{1-{r^2/R^2}}\right)dr.$$Using the positive signed equation instead of \(dz\) in the \(ds_s^2\) equation above, we get:
$$ds_s^2={dr^2\over 1-r^2/R^2}+r^2d\phi^2.$$
The derivation above was done for a spherical shell of radius \(R\) as a curved 2D surface. To generalize it to any surface, we can define \(K=1/R^2\) as the curvature parameter. Then the general infinitesimal change in a static universe can be written as:
$$ds_s^2={dr^2\over 1-Kr^2}+r^2d\phi^2.$$
Therefore, when \(K>0\) (and curvature is the same everywhere), we have a finite universe, where \(r\) cannot become larger than \(R\) as in Figure 9.2. When \(K=0\), we have a flat plane (Figure 9.1) and a negative \(K\) will correspond to an imaginary \(R\). The latter two cases may be infinite in area (which is not a simple concept, but mathematically can be modeled with \(r\) extending infinitely), or finite-area (like a cylinder is flat everywhere with \(ds_s^2={dx^2 + dy^2}\), but finite in one direction in size).
A very important issue that can be discussed now (while we are still in 2D and can actually visualize things) is that \(\overrightarrow{r}\) is tangent to the curved space at the observer’s position. In other words, it is on the gray flat surface of Figure 9.2, even when the universe if curved: \(\overrightarrow{r}=P'-A\). Therefore for the point \(P\) on a curved space, the raw coordinate \(r\) is the distance to \(P'\), not \(P\). The distance to the point \(P\) (at a specific coordinate \(r\) on the flat plane) over the curved surface (thick line in Figure 9.2) is called the proper distance and is displayed with \(l\). For the specific example of Figure 9.2, the proper distance can be calculated with: \(l=R\theta\) (\(\theta\) is in radians). Using the \(\sin\theta\) relation found above, we can find \(l\) as a function of \(r\):
$$\theta=\sin^{-1}\left({r\over R}\right)\quad\rightarrow\quad l(r)=R\sin^{-1}\left({r\over R}\right)$$
\(R\) is just an arbitrary constant and can be directly found from \(K\), so for cleaner equations, it is common practice to set \(R=1\), which gives: \(l(r)=\sin^{-1}r\). Also note that when \(R=1\), then \(l=\theta\). Generally, depending on the curvature, in a static universe the proper distance can be written as a function of the coordinate \(r\) as (from now on we are assuming \(R=1\)):
$$l(r)=\sin^{-1}(r)\quad(K>0),\quad\quad l(r)=r\quad(K=0),\quad\quad l(r)=\sinh^{-1}(r)\quad(K<0).$$With \(l\), the infinitesimal change of distance can be written in a more simpler and abstract form of
$$ds_s^2=dl^2+r^2d\phi^2.$$
Until now, we had assumed a static universe (not changing with time). But our observations so far appear to indicate that the universe is expanding (it is not static). Since there is no reason to expect the observed expansion is unique to our particular position of the universe, we expect the universe to be expanding at all points with the same rate at the same time. Therefore, to add a time dependence to our distance measurements, we can include a multiplicative scaling factor, which is a function of time: \(a(t)\). The functional form of \(a(t)\) comes from the cosmology, the physics we assume for it: general relativity, and the choice of whether the universe is uniform (‘homogeneous’) in density and curvature or inhomogeneous. In this section, the functional form of \(a(t)\) is irrelevant, so we can avoid these issues.
With this scaling factor, the proper distance will also depend on time. As the universe expands, the distance between two given points will shift to larger values. We thus define a distance measure, or coordinate, that is independent of time and thus does not ‘move’. We call it the comoving distance and display with \(\chi\) such that: \(l(r,t)=\chi(r)a(t)\). We have therefore, shifted the \(r\) dependence of the proper distance we derived above for a static universe to the comoving distance:
$$\chi(r)=\sin^{-1}(r)\quad(K>0),\quad\quad \chi(r)=r\quad(K=0),\quad\quad \chi(r)=\sinh^{-1}(r)\quad(K<0).$$
Therefore, \(\chi(r)\) is the proper distance to an object at a specific reference time: \(t=t_r\) (the \(r\) subscript signifies “reference”) when \(a(t_r)=1\). At any arbitrary moment (\(t\neq{t_r}\)) before or after \(t_r\), the proper distance to the object can be scaled with \(a(t)\).
Measuring the change of distance in a time-dependent (expanding) universe only makes sense if we can add up space and time233. But we can only add bits of space and time together if we measure them in the same units: with a conversion constant (similar to how 1000 is used to convert a kilometer into meters). Experimentally, we find strong support for the hypothesis that this conversion constant is the speed of light (or gravitational waves234) in a vacuum. This speed is postulated to be constant235 and is almost always written as \(c\). We can thus parameterize the change in distance on an expanding 2D surface as
$$ds^2=c^2dt^2-a^2(t)ds_s^2 = c^2dt^2-a^2(t)(d\chi^2+r^2d\phi^2).$$