6.3.2.1 Fourier series historical background ¶
Ever since the ancient times, the circle has been (and still is) the simplest shape for abstract comprehension. All you need is a center point and a radius and you are done. All the points on a circle are at a fixed distance from the center. However, the moment you try to connect this elegantly simple and beautiful abstract construct (the circle) with the real world (for example, compute its area or its circumference), things become really hard (ideally, impossible) because the irrational number π gets involved.
The key to understanding the Fourier series (thus the Fourier transform and finally the Discrete Fourier Transform) is our ancient desire to express everything in terms of circles or the most exceptionally simple and elegant abstract human construct. Most people prefer to say the same thing in a more ahistorical manner: to break a function into sines and cosines. As the term “ancient” in the previous sentence implies, Jean-Baptiste Joseph Fourier (1768 – 1830 A.D.) was not the first person to do this. The main reason we know this process by his name today is that he came up with an ingenious method to find the necessary coefficients (radius of) and frequencies (“speed” of rotation on) the circles for any generic (integrable) function.
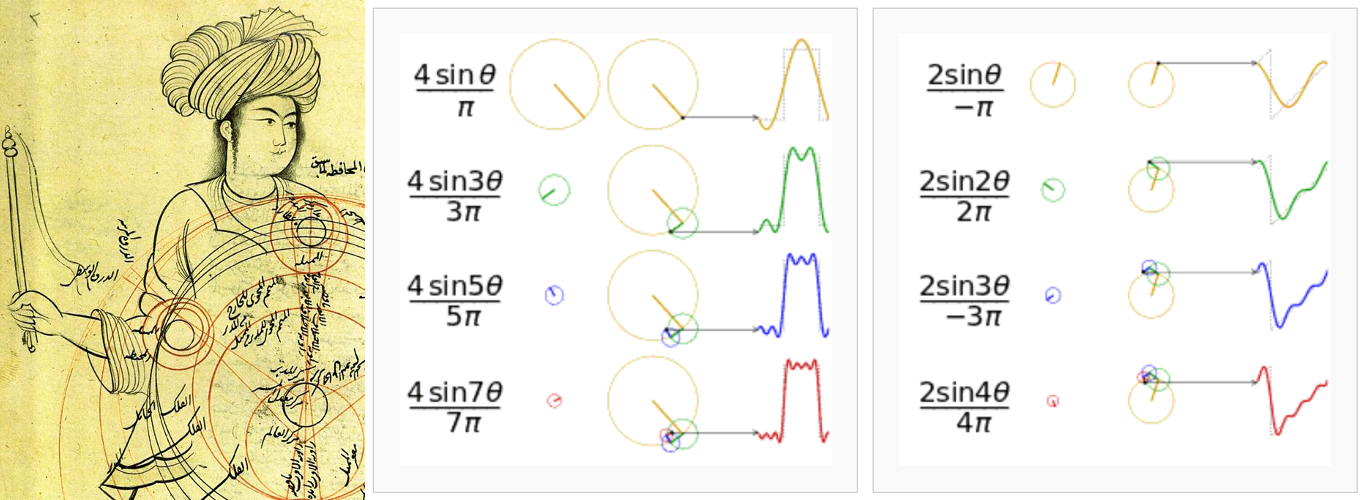
Figure 6.1: Epicycles and the Fourier series. Left: A demonstration of Mercury’s epicycles relative to the “center of the world” by Qutb al-Din al-Shirazi (1236 – 1311 A.D.) retrieved from Wikipedia. Middle and Right: How adding more epicycles (or terms in the Fourier series) will approximate functions. The right animation is also available.
Like most aspects of mathematics, this process of interpreting everything in terms of circles, began for astronomical purposes. When astronomers noticed that the orbit of Mars and other outer planets, did not appear to be a simple circle (as everything should have been in the heavens). At some point during their orbit, the revolution of these planets would become slower, stop, go back a little (in what is known as the retrograde motion) and then continue going forward again.
The correction proposed by Ptolemy (90 – 168 A.D.) was the most agreed upon. He put the planets on Epicycles or circles whose center itself rotates on a circle whose center is the earth. Eventually, as observations became more and more precise, it was necessary to add more and more epicycles in order to explain the complex motions of the planets169. Figure 6.1(Left) shows an example depiction of the epicycles of Mercury in the late 13th century.
Of course we now know that if they had abdicated the Earth from its throne in the center of the heavens and allowed the Sun to take its place, everything would become much simpler and true. But there was not enough observational evidence for changing the “professional consensus” of the time to this radical view suggested by a small minority170. So the pre-Galilean astronomers chose to keep Earth in the center and find a correction to the models (while keeping the heavens a purely “circular” order).
The main reason we are giving this historical background which might appear off topic is to give historical evidence that while such “approximations” do work and are very useful for pragmatic reasons (like measuring the calendar from the movement of astronomical bodies). They offer no physical insight. The astronomers who were involved with the Ptolemaic world view had to add a huge number of epicycles during the centuries after Ptolemy in order to explain more accurate observations. Finally the death knell of this world-view was Galileo’s observations with his new instrument (the telescope). So the physical insight, which is what Astronomers and Physicists are interested in (as opposed to Mathematicians and Engineers who just like proving and optimizing or calculating!) comes from being creative and not limiting ourselves to such approximations. Even when they work.