6.3.2.7 Sampling theorem ¶
Our mathematical functions are continuous, however, our data collecting and measuring tools are discrete. Here we want to give a mathematical formulation for digitizing the continuous mathematical functions so that later, we can retrieve the continuous function from the digitized recorded input. Assuming that we have a continuous function \(f(l)\), then we can define \(f_s(l)\) as the ‘sampled’ \(f(l)\) through the Dirac comb (see Dirac delta and comb):
$$f_s(l)=f(l){\rm III}_P=\displaystyle\sum_{n=-\infty}^{\infty}f(l)\delta(l-nP) $$
The discrete data-element \(f_k\) (for example, a pixel in an image), where \(k\) is an integer, can thus be represented as:
$$f_k=\int_{-\infty}^{\infty}f_s(l)dl=\int_{-\infty}^{\infty}f(l)\delta(l-kP)dt=f(kP)$$
Note that in practice, our discrete data points are not found in this fashion. Each detector pixel (in an image for example) has an area and averages the signal it receives over that area, not a mathematical point as the Dirac \(\delta\) function defines. However, as long as the variation in the signal over one detector pixel is not significant, this can be a good approximation. Having put this issue to the side, we can now try to find the relation between the Fourier transforms of the un-sampled \(f(l)\) and the sampled \(f_s(l)\). For a more clear notation, let’s define:
$$F_s(\omega)\equiv{\cal F}[f_s]$$
$$D(\omega)\equiv{\cal F}[{\rm III}_P]$$
Then using the Convolution theorem (see Convolution theorem), \(F_s(\omega)\) can be written as:
$$F_s(\omega)={\cal F}[f(l){\rm III}_P]=F(\omega){\ast}D(\omega)$$
Finally, from the definition of convolution and the Fourier transform of the Dirac comb (see Dirac delta and comb), we get:
$$\eqalign{ F_s(\omega) &= \int_{-\infty}^{\infty}F(\omega)D(\omega-\mu)d\mu \cr &= {1\over P}\displaystyle\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}F(\omega)\delta\left(\omega-\mu-{2{\pi}n\over P}\right)d\mu \cr &= {1\over P}\displaystyle\sum_{n=-\infty}^{\infty}F\left( \omega-{2{\pi}n\over P}\right).\cr } $$
\(F(\omega)\) was only a simple function, see Figure 6.3(left). However, from the sampled Fourier transform function we see that \(F_s(\omega)\) is the superposition of infinite copies of \(F(\omega)\) that have been shifted, see Figure 6.3(right). From the equation, it is clear that the shift in each copy is \(2\pi/P\).
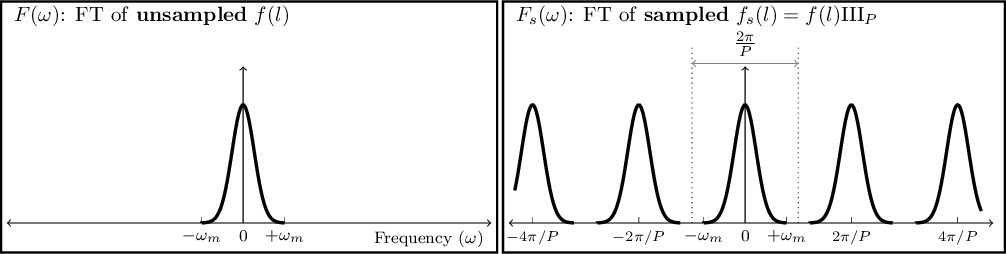
Figure 6.3: Sampling causes infinite repetition in the frequency domain. FT is an abbreviation for ‘Fourier transform’. \(\omega_m\) represents the maximum frequency present in the input. \(F(\omega)\) is only symmetric on both sides of 0 when the input is real (not complex). In general \(F(\omega)\) is complex and thus cannot be simply plotted like this. Here we have assumed a real Gaussian \(f(t)\) which has produced a Gaussian \(F(\omega)\).
The input \(f(l)\) can have any distribution of frequencies in it. In the example of Figure 6.3(left), the input consisted of a range of frequencies equal to \(\Delta\omega=2\omega_m\). Fortunately as Figure 6.3(right) shows, the assumed pixel size (\(P\)) we used to sample this hypothetical function was such that \(2\pi/P>\Delta\omega\). The consequence is that each copy of \(F(\omega)\) has become completely separate from the surrounding copies. Such a digitized (sampled) data set is thus called over-sampled. When \(2\pi/P=\Delta\omega\), \(P\) is just small enough to finely separate even the largest frequencies in the input signal and thus it is known as critically-sampled. Finally if \(2\pi/P<\Delta\omega\) we are dealing with an under-sampled data set. In an under-sampled data set, the separate copies of \(F(\omega)\) are going to overlap and this will deprive us of recovering high constituent frequencies of \(f(l)\). The effects of under-sampling in an image with high rates of change (for example, a brick wall imaged from a distance) can clearly be visually seen and is known as aliasing.
When the input \(f(l)\) is composed of a finite range of frequencies, \(f(l)\) is known as a band-limited function. The example in Figure 6.3(left) was a nice demonstration of such a case: for all \(\omega<-\omega_m\) or \(\omega>\omega_m\), we have \(F(\omega)=0\). Therefore, when the input function is band-limited and our detector’s pixels are placed such that we have critically (or over-) sampled it, then we can exactly reproduce the continuous \(f(l)\) from the discrete or digitized samples. To do that, we just have to isolate one copy of \(F(\omega)\) from the infinite copies and take its inverse Fourier transform.
This ability to exactly reproduce the continuous input from the sampled or digitized data leads us to the sampling theorem which connects the inherent property of the continuous signal (its maximum frequency) to that of the detector (the spacing between its pixels). The sampling theorem states that the full (continuous) signal can be recovered when the pixel size (\(P\)) and the maximum constituent frequency in the signal (\(\omega_m\)) have the following relation186:
$${2\pi\over P}>2\omega_m$$
This relation was first formulated by Harry Nyquist (1889 – 1976 A.D.) in 1928 and formally proved in 1949 by Claude E. Shannon (1916 – 2001 A.D.) in what is now known as the Nyquist-Shannon sampling theorem. In signal processing, the signal is produced (synthesized) by a transmitter and is received and de-coded (analyzed) by a receiver. Therefore producing a band-limited signal is necessary.
In astronomy, we do not produce the shapes of our targets, we are only observers. Galaxies can have any shape and size, therefore ideally, our signal is not band-limited. However, since we are always confined to observing through an aperture, the aperture will cause a point source (for which \(\omega_m=\infty\)) to be spread over several pixels. This spread is quantitatively known as the point spread function or PSF. This spread does blur the image which is undesirable; however, for this analysis it produces the positive outcome that there will be a finite \(\omega_m\). Though we should caution that any detector will have noise which will add lots of very high frequency (ideally infinite) changes between the pixels. However, the coefficients of those noise frequencies are usually exceedingly small.