15.6 CROSSTABS
CROSSTABS
/TABLES=var_list BY var_list [BY var_list]…
/MISSING={TABLE,INCLUDE,REPORT}
/FORMAT={TABLES,NOTABLES}
{AVALUE,DVALUE}
/CELLS={COUNT,ROW,COLUMN,TOTAL,EXPECTED,RESIDUAL,SRESIDUAL,
ASRESIDUAL,ALL,NONE}
/COUNT={ASIS,CASE,CELL}
{ROUND,TRUNCATE}
/STATISTICS={CHISQ,PHI,CC,LAMBDA,UC,BTAU,CTAU,RISK,GAMMA,D,
KAPPA,ETA,CORR,ALL,NONE}
/BARCHART
(Integer mode.)
/VARIABLES=var_list (low,high)…
The CROSSTABS procedure displays crosstabulation
tables requested by the user. It can calculate several statistics for
each cell in the crosstabulation tables. In addition, a number of
statistics can be calculated for each table itself.
The TABLES subcommand is used to specify the tables to be reported. Any
number of dimensions is permitted, and any number of variables per
dimension is allowed. The TABLES subcommand may be repeated as many
times as needed. This is the only required subcommand in general
mode.
Occasionally, one may want to invoke a special mode called integer
mode. Normally, in general mode, PSPP automatically determines
what values occur in the data. In integer mode, the user specifies the
range of values that the data assumes. To invoke this mode, specify the
VARIABLES subcommand, giving a range of data values in parentheses for
each variable to be used on the TABLES subcommand. Data values inside
the range are truncated to the nearest integer, then assigned to that
value. If values occur outside this range, they are discarded. When it
is present, the VARIABLES subcommand must precede the TABLES
subcommand.
In general mode, numeric and string variables may be specified on TABLES. In integer mode, only numeric variables are allowed.
The MISSING subcommand determines the handling of user-missing values.
When set to TABLE, the default, missing values are dropped on a table by
table basis. When set to INCLUDE, user-missing values are included in
tables and statistics. When set to REPORT, which is allowed only in
integer mode, user-missing values are included in tables but marked with
a footnote and excluded from statistical calculations.
The FORMAT subcommand controls the characteristics of the
crosstabulation tables to be displayed. It has a number of possible
settings:
TABLES, the default, causes crosstabulation tables to be output.NOTABLES, which is equivalent toCELLS=NONE, suppresses them.AVALUE, the default, causes values to be sorted in ascending order.DVALUEasserts a descending sort order.
The CELLS subcommand controls the contents of each cell in the displayed
crosstabulation table. The possible settings are:
- COUNT
Frequency count.
- ROW
Row percent.
- COLUMN
Column percent.
- TOTAL
Table percent.
- EXPECTED
Expected value.
- RESIDUAL
Residual.
- SRESIDUAL
Standardized residual.
- ASRESIDUAL
Adjusted standardized residual.
- ALL
All of the above.
- NONE
Suppress cells entirely.
‘/CELLS’ without any settings specified requests COUNT, ROW,
COLUMN, and TOTAL.
If CELLS is not specified at all then only COUNT
is selected.
By default, crosstabulation and statistics use raw case weights,
without rounding. Use the /COUNT subcommand to perform
rounding: CASE rounds the weights of individual weights as cases are
read, CELL rounds the weights of cells within each crosstabulation
table after it has been constructed, and ASIS explicitly specifies the
default non-rounding behavior. When rounding is requested, ROUND, the
default, rounds to the nearest integer and TRUNCATE rounds toward
zero.
The STATISTICS subcommand selects statistics for computation:
- CHISQ ¶
-
Pearson chi-square, likelihood ratio, Fisher’s exact test, continuity correction, linear-by-linear association.
- PHI
Phi.
- CC
Contingency coefficient.
- LAMBDA
Lambda.
- UC
Uncertainty coefficient.
- BTAU
Tau-b.
- CTAU
Tau-c.
- RISK
Risk estimate.
- GAMMA
Gamma.
- D
Somers’ D.
- KAPPA
Cohen’s Kappa.
- ETA
Eta.
- CORR
Spearman correlation, Pearson’s r.
- ALL
All of the above.
- NONE
No statistics.
Selected statistics are only calculated when appropriate for the statistic. Certain statistics require tables of a particular size, and some statistics are calculated only in integer mode.
‘/STATISTICS’ without any settings selects CHISQ. If the
STATISTICS subcommand is not given, no statistics are calculated.
The ‘/BARCHART’ subcommand produces a clustered bar chart for the first two variables on each table. If a table has more than two variables, the counts for the third and subsequent levels are aggregated and the chart is produced as if there were only two variables.
Please note: Currently the implementation of CROSSTABS has the
following limitations:
- Significance of some directional measures is not calculated.
- Asymptotic standard error is not calculated for Goodman and Kruskal’s tau or symmetric Somers’ d.
- Approximate T is not calculated for symmetric uncertainty coefficient.
Fixes for any of these deficiencies would be welcomed.
15.6.1 Crosstabs Example
A researcher wishes to know if, in an industry, a person’s sex is related to the person’s occupation. To investigate this, she has determined that the personnel.sav is a representative, randomly selected sample of persons. The researcher’s null hypothesis is that a person’s sex has no relation to a person’s occupation. She uses a chi-squared test of independence to investigate the hypothesis.
get file="personnel.sav". crosstabs /tables= occupation by sex /cells = count expected /statistics=chisq. |
Example 15.3: Running crosstabs on the sex and occupation variables
The syntax in Example 15.3 conducts a chi-squared test of independence.
The line /tables = occupation by sex indicates that occupation
and sex are the variables to be tabulated. To do this using the graphic user interface
you must place these variable names respectively in the ‘Row’ and
‘Column’ fields as shown in Screenshot 15.3.
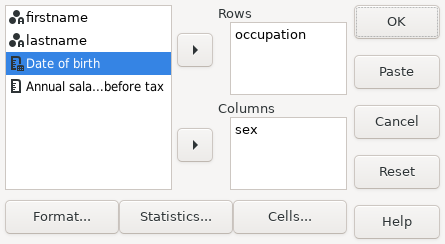 |
Screenshot 15.3: The Crosstabs dialog box with the sex and occupation variables selected
Similarly, the ‘Cells’ button shows a dialog box to select the count
and expected options. All other cell options can be deselected for this
test.
You would use the ‘Format’ and ‘Statistics’ buttons to select options
for the FORMAT and STATISTICS subcommands. In this example,
the ‘Statistics’ requires only the ‘Chisq’ option to be checked. All
other options should be unchecked. No special settings are required from the
‘Format’ dialog.
As shown in Results 15.1 CROSSTABS generates a contingency table
containing the observed count and the expected count of each sex and each
occupation. The expected count is the count which would be observed if the
null hypothesis were true.
The significance of the Pearson Chi-Square value is very much larger than the normally accepted value of 0.05 and so one cannot reject the null hypothesis. Thus the researcher must conclude that a person’s sex has no relation to the person’s occupation.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Results 15.1: The results of a test of independence between sex and occupation