3.4 A parameterizable segmented mirror model

This section shows how to take advantages of the hierarchical design feature of Goptical to write your own parameterizable optical component models. The code of a segmented mirror component model is presented and this new component is used as the primary mirror in a Ritchey-Chretien telescope design.

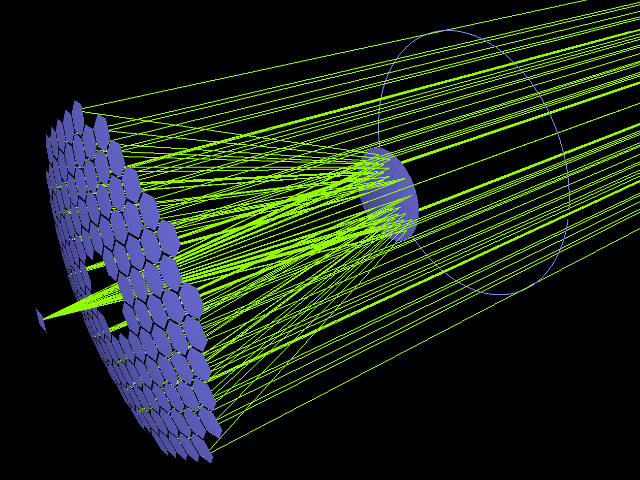
3d layout of a Ritchey-Chretien telescope with segmented primary mirror (X3D output)

3.4.1 Writing the component model class

The segmented mirror model uses hexagonal segments and takes a surface curve model, an aperture shape model, segment size and segment separation as parameters. We start the definition of our model class which inherits from the Sys::Group class:

// code from examples/segmented_mirror/segmented.cc:62

class HexSegMirror : public Sys::Group
{
public:

  HexSegMirror(const Math::VectorPair3 &pos,
               const const_ref<Curve::Base> &curve,
               const const_ref<Shape::Base> &shape,
               double seg_radius, double separation)
    : Sys::Group(pos)
  {

When the model is instantiated, all hexagonal mirrors need to be created from the constructor. We use two loops in order to build the hexagonal mirror tessellation:

    if (seg_radius > separation)
      throw(Error("overlapping segments"));

    // sqrt(3)/2
    static const double sqrt_3_2 = 0.86602540378443864676;

    // hexagonal tessellation
    int x_count = ceil(shape->max_radius() / (separation * 1.5));
    int y_count = ceil(shape->max_radius() / (separation * 2 * sqrt_3_2));

    for (int x = -x_count; x <= x_count ; x++)
      {
        for (int y = -y_count; y <= y_count ; y++)
          {
            // find segment mirror 2d position
            double yoffset = x % 2 ? separation * sqrt_3_2 : 0;
            Math::Vector2 p(x * separation * 1.5,
                              yoffset + y * separation * 2 * sqrt_3_2 );

The aperture shape is then used to check if a segment mirror must exist at each location:

            // skip if segment center is outside main shape
            if (!shape->inside(p))
              continue;

The segment mirror curve must take into account the offset from the main mirror origin. We also decide to subtract the sagitta offset from the segment curve and add it to its Z component position instead; this allows its origin to lie on the segment surface, which may be more convenient when tilting the segment. The Curve::Composer class is used here to apply required transformations to the model curve passed as a parameter:

            // find curve z offset at segment center to shift both
            // curve and segment in opposite directions.
            double z_offset = curve->sagitta(p);

            // create a composer curve for this segment and use it to translate main curve
            ref<Curve::Composer> seg_curve = ref<Curve::Composer>::create();

            seg_curve->add_curve(curve).xy_translate(-p).z_offset(-z_offset);

The segment mirror is then created and added to the model group:

            // create a segment mirror with hexagonal shape and translated curve
            ref<Sys::Mirror> seg = ref<Sys::Mirror>::create(Math::Vector3(p, z_offset), seg_curve,
                                             ref<Shape::RegularPolygon>::create(seg_radius, 6));

            // attach the new segment to our group component
            add(seg);

We finally add some code to keep track of the segments so that they can be accessed (and modified) separately after model instantiation:

            // keep a pointer to this new segment
            _segments.push_back(seg.ptr());
          }
      }
  }

  size_t get_segments_count() const
  {
    return _segments.size();
  }

  Sys::Mirror & get_segment(size_t i) const
  {
    return *_segments.at(i);
  }

private:
  std::vector<Sys::Mirror *> _segments;
};

This model class is less than 70 lines long, including comments.

3.4.2 Using the model in Ritchey-Chretien design

Our new model can now be used like other component models in optical systems and groups. We use it here with a ring aperture shape and conic curvature to model the primary mirror of a Ritchey-Chretien telescope:

  Sys::System             sys;

  // Ring shaped segmented mirror with conic curve
  HexSegMirror            primary(Math::Vector3(0, 0, 800),
                                  ref<Curve::Conic>::create(-1600, -1.0869),
                                  ref<Shape::Ring>::create(300, 85),
                                  28, 30);
  sys.add(primary);

  Sys::Mirror             secondary(Math::VectorPair3(0, 0, 225, 0, 0, -1), 675, -5.0434, 100);
  sys.add(secondary);

  Sys::Image              image(Math::VectorPair3(0, 0, 900), 15);
  sys.add(image);

  Sys::Stop               stop(Math::vector3_0, 300);
  sys.add(stop);
  sys.set_entrance_pupil(stop);

  Sys::SourcePoint        source(Sys::SourceAtInfinity, Math::vector3_001);
  sys.add(source);