Chebyshev Approximations¶
This chapter describes routines for computing Chebyshev approximations
to univariate functions. A Chebyshev approximation is a truncation of
the series 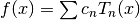 , where the Chebyshev
polynomials
, where the Chebyshev
polynomials 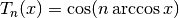 provide an orthogonal
basis of polynomials on the interval
provide an orthogonal
basis of polynomials on the interval ![[-1,1]](_images/math/9d7700522727dac61e0f0c6d894326947027e00f.png) with the weight
function
with the weight
function 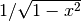 .
The first few Chebyshev polynomials are,
.
The first few Chebyshev polynomials are,
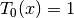 ,
, 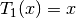 ,
, 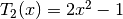 .
For further information see Abramowitz & Stegun, Chapter 22.
.
For further information see Abramowitz & Stegun, Chapter 22.
The functions described in this chapter are declared in the header file
gsl_chebyshev.h.
Definitions¶
-
type gsl_cheb_series¶
A Chebyshev series is stored using the following structure:
typedef struct { double * c; /* coefficients c[0] .. c[order] */ int order; /* order of expansion */ double a; /* lower interval point */ double b; /* upper interval point */ ... } gsl_cheb_series
The approximation is made over the range ![[a,b]](_images/math/c47bfde07e072efe45e71eb8b5e6891be77ec2df.png) using
using
order + 1 terms, including the coefficient ![c[0]](_images/math/d526a7bde7b918af0a8715eb4112f289fc1d1c39.png) . The series
is computed using the following convention,
. The series
is computed using the following convention,
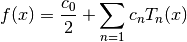
which is needed when accessing the coefficients directly.
Creation and Calculation of Chebyshev Series¶
-
gsl_cheb_series *gsl_cheb_alloc(const size_t n)¶
This function allocates space for a Chebyshev series of order
nand returns a pointer to a newgsl_cheb_seriesstruct.
-
void gsl_cheb_free(gsl_cheb_series *cs)¶
This function frees a previously allocated Chebyshev series
cs.
-
int gsl_cheb_init(gsl_cheb_series *cs, const gsl_function *f, const double a, const double b)¶
This function computes the Chebyshev approximation
csfor the functionfover the range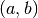 to the previously specified
order. The computation of the Chebyshev approximation is an
to the previously specified
order. The computation of the Chebyshev approximation is an
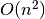 process, and requires
process, and requires  function evaluations.
function evaluations.
Auxiliary Functions¶
The following functions provide information about an existing Chebyshev series.
-
size_t gsl_cheb_order(const gsl_cheb_series *cs)¶
This function returns the order of Chebyshev series
cs.
-
size_t gsl_cheb_size(const gsl_cheb_series *cs)¶
-
double *gsl_cheb_coeffs(const gsl_cheb_series *cs)¶
These functions return the size of the Chebyshev coefficient array
c[]and a pointer to its location in memory for the Chebyshev seriescs.
Chebyshev Series Evaluation¶
-
double gsl_cheb_eval(const gsl_cheb_series *cs, double x)¶
This function evaluates the Chebyshev series
csat a given pointx.
-
int gsl_cheb_eval_err(const gsl_cheb_series *cs, const double x, double *result, double *abserr)¶
This function computes the Chebyshev series
csat a given pointx, estimating both the seriesresultand its absolute errorabserr. The error estimate is made from the first neglected term in the series.
-
double gsl_cheb_eval_n(const gsl_cheb_series *cs, size_t order, double x)¶
This function evaluates the Chebyshev series
csat a given pointx, to (at most) the given orderorder.
-
int gsl_cheb_eval_n_err(const gsl_cheb_series *cs, const size_t order, const double x, double *result, double *abserr)¶
This function evaluates a Chebyshev series
csat a given pointx, estimating both the seriesresultand its absolute errorabserr, to (at most) the given orderorder. The error estimate is made from the first neglected term in the series.
Derivatives and Integrals¶
The following functions allow a Chebyshev series to be differentiated or integrated, producing a new Chebyshev series. Note that the error estimate produced by evaluating the derivative series will be underestimated due to the contribution of higher order terms being neglected.
-
int gsl_cheb_calc_deriv(gsl_cheb_series *deriv, const gsl_cheb_series *cs)¶
This function computes the derivative of the series
cs, storing the derivative coefficients in the previously allocatedderiv. The two seriescsandderivmust have been allocated with the same order.
-
int gsl_cheb_calc_integ(gsl_cheb_series *integ, const gsl_cheb_series *cs)¶
This function computes the integral of the series
cs, storing the integral coefficients in the previously allocatedinteg. The two seriescsandintegmust have been allocated with the same order. The lower limit of the integration is taken to be the left hand end of the rangea.
Examples¶
The following example program computes Chebyshev approximations to a step function. This is an extremely difficult approximation to make, due to the discontinuity, and was chosen as an example where approximation error is visible. For smooth functions the Chebyshev approximation converges extremely rapidly and errors would not be visible.
#include <stdio.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_chebyshev.h>
double
f (double x, void *p)
{
(void)(p); /* avoid unused parameter warning */
if (x < 0.5)
return 0.25;
else
return 0.75;
}
int
main (void)
{
int i, n = 10000;
gsl_cheb_series *cs = gsl_cheb_alloc (40);
gsl_function F;
F.function = f;
F.params = 0;
gsl_cheb_init (cs, &F, 0.0, 1.0);
for (i = 0; i < n; i++)
{
double x = i / (double)n;
double r10 = gsl_cheb_eval_n (cs, 10, x);
double r40 = gsl_cheb_eval (cs, x);
printf ("%g %g %g %g\n",
x, GSL_FN_EVAL (&F, x), r10, r40);
}
gsl_cheb_free (cs);
return 0;
}
Fig. 26 shows output from the program with the original function, 10-th order
approximation and 40-th order approximation, all sampled at intervals of
0.001 in  .
.
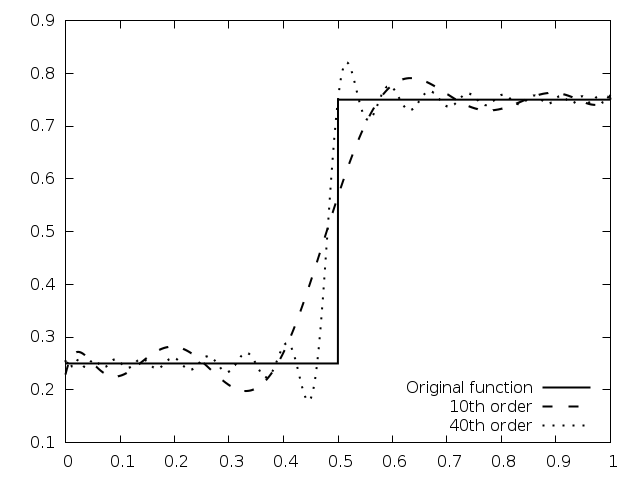
Fig. 26 Chebyshev approximations to a step function¶
References and Further Reading¶
The following paper describes the use of Chebyshev series,
R. Broucke, “Ten Subroutines for the Manipulation of Chebyshev Series [C1] (Algorithm 446)”. Communications of the ACM 16(4), 254–256 (1973)