Complex Numbers¶
The functions described in this chapter provide support for complex numbers. The algorithms take care to avoid unnecessary intermediate underflows and overflows, allowing the functions to be evaluated over as much of the complex plane as possible.
For multiple-valued functions the branch cuts have been chosen to follow the conventions of Abramowitz and Stegun. The functions return principal values which are the same as those in GNU Calc, which in turn are the same as those in “Common Lisp, The Language (Second Edition)” 1 and the HP-28/48 series of calculators.
The complex types are defined in the header file gsl_complex.h,
while the corresponding complex functions and arithmetic operations are
defined in gsl_complex_math.h.
Representation of complex numbers¶
Complex numbers are represented using the type gsl_complex. The
default interface defines gsl_complex as:
typedef struct
{
double dat[2];
} gsl_complex;
The real and imaginary part are stored in contiguous elements of a two
element array. This eliminates any padding between the real and
imaginary parts, dat[0] and dat[1], allowing the struct to
be mapped correctly onto packed complex arrays.
If a C compiler is available which supports the C11 standard,
and the <complex.h> header file is included prior to gsl_complex.h,
then gsl_complex will be defined to be the native C complex type:
typedef double complex gsl_complex
This allows users to use gsl_complex in ordinary operations such as:
gsl_complex x = 2 + 5 * I;
gsl_complex y = x + (3 - 4*I);
Important
Native C support for complex numbers was introduced in the C99 standard,
and additional functionality was added in C11. When <complex.h>
is included in a user’s program prior to gsl_complex.h,
GSL uses the new C11 functionality to define the GSL_REAL and
GSL_IMAG macros. It does not appear possible to properly define
these macros using the C99 standard, and so using a C99 compiler will not define
gsl_complex to the native complex type.
Some compilers, such as the gcc 4.8 series implement only a portion of the C11
standard and so they may fail to correctly compile GSL code when a user tries
to turn on native complex functionality. A workaround for this issue is to
either remove <complex.h> from the include list, or add
-DGSL_COMPLEX_LEGACY to the compiler flags, which will use the older
struct-based definition of gsl_complex.
Complex number macros¶
The following C macros offer convenient ways to manipulate complex numbers.
-
GSL_REAL(z)¶
-
GSL_IMAG(z)¶
These macros return a memory location (lvalue) corresponding to the real and imaginary parts respectively of the complex number
z. This allows users to perform operations like:gsl_complex x, y; GSL_REAL(x) = 4; GSL_IMAG(x) = 2; GSL_REAL(y) = GSL_REAL(x); GSL_IMAG(y) = GSL_REAL(x);
In other words, these macros can both read and write to the real and imaginary parts of a complex variable.
-
GSL_SET_COMPLEX(zp, x, y)¶
This macro uses the Cartesian components (
x,y) to set the real and imaginary parts of the complex number pointed to byzp. For example:GSL_SET_COMPLEX(&z, 3, 4)
sets
 to be
to be 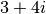 .
.
Assigning complex numbers¶
-
gsl_complex gsl_complex_rect(double x, double y)¶
This function uses the rectangular Cartesian components
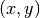 to return the complex number
to return the complex number 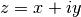 .
An inline version of this function is used when
.
An inline version of this function is used when HAVE_INLINEis defined.
Properties of complex numbers¶
-
double gsl_complex_arg(gsl_complex z)¶
This function returns the argument of the complex number
z,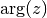 , where
, where 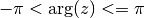 .
.
-
double gsl_complex_abs(gsl_complex z)¶
This function returns the magnitude of the complex number
z,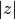 .
.
Complex arithmetic operators¶
-
gsl_complex gsl_complex_add(gsl_complex a, gsl_complex b)¶
This function returns the sum of the complex numbers
aandb,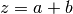 .
.
-
gsl_complex gsl_complex_sub(gsl_complex a, gsl_complex b)¶
This function returns the difference of the complex numbers
aandb,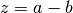 .
.
-
gsl_complex gsl_complex_mul(gsl_complex a, gsl_complex b)¶
This function returns the product of the complex numbers
aandb,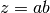 .
.
-
gsl_complex gsl_complex_div(gsl_complex a, gsl_complex b)¶
This function returns the quotient of the complex numbers
aandb,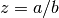 .
.
-
gsl_complex gsl_complex_add_real(gsl_complex a, double x)¶
This function returns the sum of the complex number
aand the real numberx,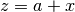 .
.
-
gsl_complex gsl_complex_sub_real(gsl_complex a, double x)¶
This function returns the difference of the complex number
aand the real numberx,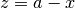 .
.
-
gsl_complex gsl_complex_mul_real(gsl_complex a, double x)¶
This function returns the product of the complex number
aand the real numberx,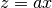 .
.
-
gsl_complex gsl_complex_div_real(gsl_complex a, double x)¶
This function returns the quotient of the complex number
aand the real numberx,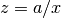 .
.
-
gsl_complex gsl_complex_add_imag(gsl_complex a, double y)¶
This function returns the sum of the complex number
aand the imaginary number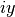 ,
, 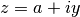 .
.
-
gsl_complex gsl_complex_sub_imag(gsl_complex a, double y)¶
This function returns the difference of the complex number
aand the imaginary number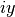 ,
, 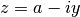 .
.
-
gsl_complex gsl_complex_mul_imag(gsl_complex a, double y)¶
This function returns the product of the complex number
aand the imaginary number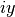 ,
, 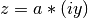 .
.
-
gsl_complex gsl_complex_div_imag(gsl_complex a, double y)¶
This function returns the quotient of the complex number
aand the imaginary number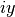 ,
, 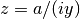 .
.
-
gsl_complex gsl_complex_conjugate(gsl_complex z)¶
This function returns the complex conjugate of the complex number
z,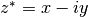 .
.
Elementary Complex Functions¶
-
gsl_complex gsl_complex_sqrt(gsl_complex z)¶
This function returns the square root of the complex number
z,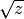 . The branch cut is the negative real axis. The result
always lies in the right half of the complex plane.
. The branch cut is the negative real axis. The result
always lies in the right half of the complex plane.
-
gsl_complex gsl_complex_sqrt_real(double x)¶
This function returns the complex square root of the real number
x, wherexmay be negative.
-
gsl_complex gsl_complex_pow(gsl_complex z, gsl_complex a)¶
The function returns the complex number
zraised to the complex powera,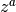 . This is computed as
. This is computed as 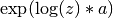 using complex logarithms and complex exponentials.
using complex logarithms and complex exponentials.
-
gsl_complex gsl_complex_pow_real(gsl_complex z, double x)¶
This function returns the complex number
zraised to the real powerx,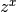 .
.
-
gsl_complex gsl_complex_exp(gsl_complex z)¶
This function returns the complex exponential of the complex number
z,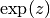 .
.
-
gsl_complex gsl_complex_log(gsl_complex z)¶
This function returns the complex natural logarithm (base
 ) of
the complex number
) of
the complex number z,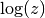 . The branch cut is the
negative real axis.
. The branch cut is the
negative real axis.
Complex Trigonometric Functions¶
-
gsl_complex gsl_complex_sin(gsl_complex z)¶
This function returns the complex sine of the complex number
z,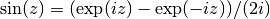 .
.
-
gsl_complex gsl_complex_cos(gsl_complex z)¶
This function returns the complex cosine of the complex number
z,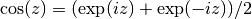 .
.
-
gsl_complex gsl_complex_tan(gsl_complex z)¶
This function returns the complex tangent of the complex number
z,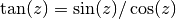 .
.
-
gsl_complex gsl_complex_sec(gsl_complex z)¶
This function returns the complex secant of the complex number
z,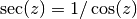 .
.
Inverse Complex Trigonometric Functions¶
-
gsl_complex gsl_complex_arcsin(gsl_complex z)¶
This function returns the complex arcsine of the complex number
z,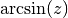 . The branch cuts are on the real axis, less than
. The branch cuts are on the real axis, less than 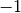 and greater than
and greater than 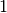 .
.
-
gsl_complex gsl_complex_arcsin_real(double z)¶
This function returns the complex arcsine of the real number
z,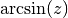 . For
. For  between
between 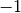 and
and 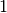 , the
function returns a real value in the range
, the
function returns a real value in the range ![[-\pi/2,\pi/2]](_images/math/71670a6b0d66e6ed26712f0312a4b0ea5b28f467.png) . For
. For
 less than
less than 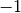 the result has a real part of
the result has a real part of 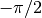 and a positive imaginary part. For
and a positive imaginary part. For  greater than
greater than 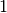 the
result has a real part of
the
result has a real part of 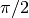 and a negative imaginary part.
and a negative imaginary part.
-
gsl_complex gsl_complex_arccos(gsl_complex z)¶
This function returns the complex arccosine of the complex number
z,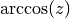 . The branch cuts are on the real axis, less than
. The branch cuts are on the real axis, less than 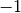 and greater than
and greater than 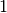 .
.
-
gsl_complex gsl_complex_arccos_real(double z)¶
This function returns the complex arccosine of the real number
z,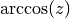 . For
. For  between
between 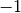 and
and 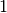 , the
function returns a real value in the range
, the
function returns a real value in the range ![[0,\pi]](_images/math/ddfadf82cb98326a6692198ac64c3da6f7e2ac07.png) . For
. For  less than
less than 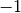 the result has a real part of
the result has a real part of 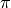 and a
negative imaginary part. For
and a
negative imaginary part. For  greater than
greater than 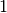 the result
is purely imaginary and positive.
the result
is purely imaginary and positive.
-
gsl_complex gsl_complex_arctan(gsl_complex z)¶
This function returns the complex arctangent of the complex number
z, . The branch cuts are on the imaginary axis,
below
. The branch cuts are on the imaginary axis,
below 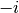 and above
and above 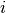 .
.
-
gsl_complex gsl_complex_arcsec(gsl_complex z)¶
This function returns the complex arcsecant of the complex number
z,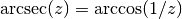 .
.
-
gsl_complex gsl_complex_arcsec_real(double z)¶
This function returns the complex arcsecant of the real number
z,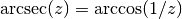 .
.
-
gsl_complex gsl_complex_arccsc(gsl_complex z)¶
This function returns the complex arccosecant of the complex number
z,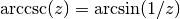 .
.
Complex Hyperbolic Functions¶
-
gsl_complex gsl_complex_sinh(gsl_complex z)¶
This function returns the complex hyperbolic sine of the complex number
z,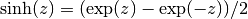 .
.
-
gsl_complex gsl_complex_cosh(gsl_complex z)¶
This function returns the complex hyperbolic cosine of the complex number
z,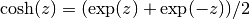 .
.
-
gsl_complex gsl_complex_tanh(gsl_complex z)¶
This function returns the complex hyperbolic tangent of the complex number
z,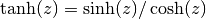 .
.
-
gsl_complex gsl_complex_sech(gsl_complex z)¶
This function returns the complex hyperbolic secant of the complex number
z,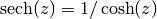 .
.
Inverse Complex Hyperbolic Functions¶
-
gsl_complex gsl_complex_arcsinh(gsl_complex z)¶
This function returns the complex hyperbolic arcsine of the complex number
z,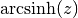 . The branch cuts are on the
imaginary axis, below
. The branch cuts are on the
imaginary axis, below 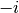 and above
and above 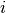 .
.
-
gsl_complex gsl_complex_arccosh(gsl_complex z)¶
This function returns the complex hyperbolic arccosine of the complex number
z,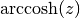 . The branch cut is on the real
axis, less than
. The branch cut is on the real
axis, less than 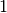 . Note that in this case we use the negative
square root in formula 4.6.21 of Abramowitz & Stegun giving
. Note that in this case we use the negative
square root in formula 4.6.21 of Abramowitz & Stegun giving
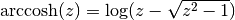 .
.
-
gsl_complex gsl_complex_arccosh_real(double z)¶
This function returns the complex hyperbolic arccosine of the real number
z,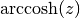 .
.
-
gsl_complex gsl_complex_arctanh(gsl_complex z)¶
This function returns the complex hyperbolic arctangent of the complex number
z,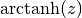 . The branch cuts are on the real
axis, less than
. The branch cuts are on the real
axis, less than 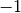 and greater than
and greater than 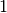 .
.
-
gsl_complex gsl_complex_arctanh_real(double z)¶
This function returns the complex hyperbolic arctangent of the real number
z,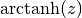 .
.
-
gsl_complex gsl_complex_arcsech(gsl_complex z)¶
This function returns the complex hyperbolic arcsecant of the complex number
z,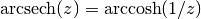 .
.
References and Further Reading¶
The implementations of the elementary and trigonometric functions are based on the following papers,
T. E. Hull, Thomas F. Fairgrieve, Ping Tak Peter Tang, “Implementing Complex Elementary Functions Using Exception Handling”, ACM Transactions on Mathematical Software, Volume 20 (1994), pp 215–244, Corrigenda, p553
T. E. Hull, Thomas F. Fairgrieve, Ping Tak Peter Tang, “Implementing the complex arcsin and arccosine functions using exception handling”, ACM Transactions on Mathematical Software, Volume 23 (1997) pp 299–335
The general formulas and details of branch cuts can be found in the following books,
Abramowitz and Stegun, Handbook of Mathematical Functions, “Circular Functions in Terms of Real and Imaginary Parts”, Formulas 4.3.55–58, “Inverse Circular Functions in Terms of Real and Imaginary Parts”, Formulas 4.4.37–39, “Hyperbolic Functions in Terms of Real and Imaginary Parts”, Formulas 4.5.49–52, “Inverse Hyperbolic Functions—relation to Inverse Circular Functions”, Formulas 4.6.14–19.
Dave Gillespie, Calc Manual, Free Software Foundation, ISBN 1-882114-18-3
Footnotes
- 1
Note that the first edition uses different definitions.
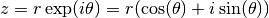 from the polar representation
(
from the polar representation
(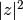 .
.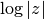 . It allows an accurate
evaluation of
. It allows an accurate
evaluation of 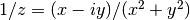 .
.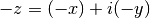 .
.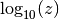 .
.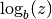 . This quantity is computed as the ratio
. This quantity is computed as the ratio
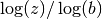 .
.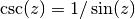 .
.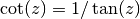 .
.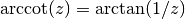 .
.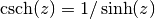 .
.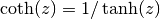 .
.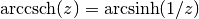 .
.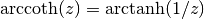 .
.