Vectors and Matrices¶
The functions described in this chapter provide a simple vector and matrix interface to ordinary C arrays. The memory management of these arrays is implemented using a single underlying type, known as a block. By writing your functions in terms of vectors and matrices you can pass a single structure containing both data and dimensions as an argument without needing additional function parameters. The structures are compatible with the vector and matrix formats used by BLAS routines.
Data types¶
All the functions are available for each of the standard data-types.
The versions for double have the prefix gsl_block,
gsl_vector and gsl_matrix. Similarly the versions for
single-precision float arrays have the prefix
gsl_block_float, gsl_vector_float and
gsl_matrix_float. The full list of available types is given
below,
Prefix |
Type |
|---|---|
gsl_block |
double |
gsl_block_float |
float |
gsl_block_long_double |
long double |
gsl_block_int |
int |
gsl_block_uint |
unsigned int |
gsl_block_long |
long |
gsl_block_ulong |
unsigned long |
gsl_block_short |
short |
gsl_block_ushort |
unsigned short |
gsl_block_char |
char |
gsl_block_uchar |
unsigned char |
gsl_block_complex |
complex double |
gsl_block_complex_float |
complex float |
gsl_block_complex_long_double |
complex long double |
Corresponding types exist for the gsl_vector and
gsl_matrix functions.
Blocks¶
For consistency all memory is allocated through a gsl_block
structure. The structure contains two components, the size of an area of
memory and a pointer to the memory. The gsl_block structure looks
like this,
-
type gsl_block¶
typedef struct { size_t size; double * data; } gsl_block;
Vectors and matrices are made by slicing an underlying block. A slice is a set of elements formed from an initial offset and a combination of indices and step-sizes. In the case of a matrix the step-size for the column index represents the row-length. The step-size for a vector is known as the stride.
The functions for allocating and deallocating blocks are defined in
gsl_block.h.
Block allocation¶
The functions for allocating memory to a block follow the style of
malloc and free. In addition they also perform their own
error checking. If there is insufficient memory available to allocate a
block then the functions call the GSL error handler (with an error
number of GSL_ENOMEM) in addition to returning a null
pointer. Thus if you use the library error handler to abort your program
then it isn’t necessary to check every alloc.
-
gsl_block *gsl_block_alloc(size_t n)¶
This function allocates memory for a block of
ndouble-precision elements, returning a pointer to the block struct. The block is not initialized and so the values of its elements are undefined. Use the functiongsl_block_calloc()if you want to ensure that all the elements are initialized to zero.Zero-sized requests are valid and return a non-null result. A null pointer is returned if insufficient memory is available to create the block.
-
gsl_block *gsl_block_calloc(size_t n)¶
This function allocates memory for a block and initializes all the elements of the block to zero.
-
void gsl_block_free(gsl_block *b)¶
This function frees the memory used by a block
bpreviously allocated withgsl_block_alloc()orgsl_block_calloc().
Reading and writing blocks¶
The library provides functions for reading and writing blocks to a file as binary data or formatted text.
-
int gsl_block_fwrite(FILE *stream, const gsl_block *b)¶
This function writes the elements of the block
bto the streamstreamin binary format. The return value is 0 for success andGSL_EFAILEDif there was a problem writing to the file. Since the data is written in the native binary format it may not be portable between different architectures.
-
int gsl_block_fread(FILE *stream, gsl_block *b)¶
This function reads into the block
bfrom the open streamstreamin binary format. The blockbmust be preallocated with the correct length since the function uses the size ofbto determine how many bytes to read. The return value is 0 for success andGSL_EFAILEDif there was a problem reading from the file. The data is assumed to have been written in the native binary format on the same architecture.
-
int gsl_block_fprintf(FILE *stream, const gsl_block *b, const char *format)¶
This function writes the elements of the block
bline-by-line to the streamstreamusing the format specifierformat, which should be one of the%g,%eor%fformats for floating point numbers and%dfor integers. The function returns 0 for success andGSL_EFAILEDif there was a problem writing to the file.
-
int gsl_block_fscanf(FILE *stream, gsl_block *b)¶
This function reads formatted data from the stream
streaminto the blockb. The blockbmust be preallocated with the correct length since the function uses the size ofbto determine how many numbers to read. The function returns 0 for success andGSL_EFAILEDif there was a problem reading from the file.
Example programs for blocks¶
The following program shows how to allocate a block,
#include <stdio.h>
#include <gsl/gsl_block.h>
int
main (void)
{
gsl_block * b = gsl_block_alloc (100);
printf ("length of block = %zu\n", b->size);
printf ("block data address = %p\n", b->data);
gsl_block_free (b);
return 0;
}
Here is the output from the program,
length of block = 100
block data address = 0x804b0d8
Vectors¶
Vectors are defined by a gsl_vector structure which describes a
slice of a block. Different vectors can be created which point to the
same block. A vector slice is a set of equally-spaced elements of an
area of memory.
The gsl_vector structure contains five components, the
size, the stride, a pointer to the memory where the elements
are stored, data, a pointer to the block owned by the vector,
block, if any, and an ownership flag, owner. The structure
is very simple and looks like this,
-
type gsl_vector¶
typedef struct { size_t size; size_t stride; double * data; gsl_block * block; int owner; } gsl_vector;
The size is simply the number of vector elements. The range of
valid indices runs from 0 to size-1. The stride is the
step-size from one element to the next in physical memory, measured in
units of the appropriate datatype. The pointer data gives the
location of the first element of the vector in memory. The pointer
block stores the location of the memory block in which the vector
elements are located (if any). If the vector owns this block then the
owner field is set to one and the block will be deallocated when the
vector is freed. If the vector points to a block owned by another
object then the owner field is zero and any underlying block will not be
deallocated with the vector.
The functions for allocating and accessing vectors are defined in
gsl_vector.h.
Vector allocation¶
The functions for allocating memory to a vector follow the style of
malloc and free. In addition they also perform their own
error checking. If there is insufficient memory available to allocate a
vector then the functions call the GSL error handler (with an error
number of GSL_ENOMEM) in addition to returning a null
pointer. Thus if you use the library error handler to abort your program
then it isn’t necessary to check every alloc.
-
gsl_vector *gsl_vector_alloc(size_t n)¶
This function creates a vector of length n, returning a pointer to a newly initialized vector struct. A new block is allocated for the elements of the vector, and stored in the
blockcomponent of the vector struct. The block is “owned” by the vector, and will be deallocated when the vector is deallocated. Zero-sized requests are valid and return a non-null result.
-
gsl_vector *gsl_vector_calloc(size_t n)¶
This function allocates memory for a vector of length
nand initializes all the elements of the vector to zero.
-
void gsl_vector_free(gsl_vector *v)¶
This function frees a previously allocated vector
v. If the vector was created usinggsl_vector_alloc()then the block underlying the vector will also be deallocated. If the vector has been created from another object then the memory is still owned by that object and will not be deallocated.
Accessing vector elements¶
Unlike Fortran compilers, C compilers do not usually provide
support for range checking of vectors and matrices. 1
The functions gsl_vector_get() and
gsl_vector_set() can perform portable range checking for you and
report an error if you attempt to access elements outside the allowed
range.
The functions for accessing the elements of a vector or matrix are
defined in gsl_vector.h and declared extern inline to
eliminate function-call overhead. You must compile your program with
the preprocessor macro HAVE_INLINE defined to use these
functions.
-
GSL_RANGE_CHECK_OFF¶
If necessary you can turn off range checking completely without modifying any source files by recompiling your program with the preprocessor definition
GSL_RANGE_CHECK_OFF. Provided your compiler supports inline functions the effect of turning off range checking is to replace calls togsl_vector_get(v,i)byv->data[i*v->stride]and calls togsl_vector_set(v,i,x)byv->data[i*v->stride]=x. Thus there should be no performance penalty for using the range checking functions when range checking is turned off.
-
GSL_C99_INLINE¶
If you use a C99 compiler which requires inline functions in header files to be declared
inlineinstead ofextern inline, define the macroGSL_C99_INLINE(see Inline functions). With GCC this is selected automatically when compiling in C99 mode (-std=c99).
-
int gsl_check_range¶
If inline functions are not used, calls to the functions
gsl_vector_get()andgsl_vector_set()will link to the compiled versions of these functions in the library itself. The range checking in these functions is controlled by the global integer variablegsl_check_range. It is enabled by default—to disable it, setgsl_check_rangeto zero. Due to function-call overhead, there is less benefit in disabling range checking here than for inline functions.
-
double gsl_vector_get(const gsl_vector *v, const size_t i)¶
This function returns the
i-th element of a vectorv. Ifilies outside the allowed range of 0 tosize - 1then the error handler is invoked and 0 is returned. An inline version of this function is used whenHAVE_INLINEis defined.
-
void gsl_vector_set(gsl_vector *v, const size_t i, double x)¶
This function sets the value of the
i-th element of a vectorvtox. Ifilies outside the allowed range of 0 tosize - 1then the error handler is invoked. An inline version of this function is used whenHAVE_INLINEis defined.
-
double *gsl_vector_ptr(gsl_vector *v, size_t i)¶
-
const double *gsl_vector_const_ptr(const gsl_vector *v, size_t i)¶
These functions return a pointer to the
i-th element of a vectorv. Ifilies outside the allowed range of 0 tosize - 1then the error handler is invoked and a null pointer is returned. Inline versions of these functions are used whenHAVE_INLINEis defined.
Initializing vector elements¶
-
void gsl_vector_set_all(gsl_vector *v, double x)¶
This function sets all the elements of the vector
vto the valuex.
-
void gsl_vector_set_zero(gsl_vector *v)¶
This function sets all the elements of the vector
vto zero.
-
int gsl_vector_set_basis(gsl_vector *v, size_t i)¶
This function makes a basis vector by setting all the elements of the vector
vto zero except for thei-th element which is set to one.
Reading and writing vectors¶
The library provides functions for reading and writing vectors to a file as binary data or formatted text.
-
int gsl_vector_fwrite(FILE *stream, const gsl_vector *v)¶
This function writes the elements of the vector
vto the streamstreamin binary format. The return value is 0 for success andGSL_EFAILEDif there was a problem writing to the file. Since the data is written in the native binary format it may not be portable between different architectures.
-
int gsl_vector_fread(FILE *stream, gsl_vector *v)¶
This function reads into the vector
vfrom the open streamstreamin binary format. The vectorvmust be preallocated with the correct length since the function uses the size ofvto determine how many bytes to read. The return value is 0 for success andGSL_EFAILEDif there was a problem reading from the file. The data is assumed to have been written in the native binary format on the same architecture.
-
int gsl_vector_fprintf(FILE *stream, const gsl_vector *v, const char *format)¶
This function writes the elements of the vector
vline-by-line to the streamstreamusing the format specifierformat, which should be one of the%g,%eor%fformats for floating point numbers and%dfor integers. The function returns 0 for success andGSL_EFAILEDif there was a problem writing to the file.
-
int gsl_vector_fscanf(FILE *stream, gsl_vector *v)¶
This function reads formatted data from the stream
streaminto the vectorv. The vectorvmust be preallocated with the correct length since the function uses the size ofvto determine how many numbers to read. The function returns 0 for success andGSL_EFAILEDif there was a problem reading from the file.
Vector views¶
In addition to creating vectors from slices of blocks it is also possible to slice vectors and create vector views. For example, a subvector of another vector can be described with a view, or two views can be made which provide access to the even and odd elements of a vector.
-
type gsl_vector_view¶
-
type gsl_vector_const_view¶
A vector view is a temporary object, stored on the stack, which can be used to operate on a subset of vector elements. Vector views can be defined for both constant and non-constant vectors, using separate types that preserve constness. A vector view has the type
gsl_vector_viewand a constant vector view has the typegsl_vector_const_view. In both cases the elements of the view can be accessed as agsl_vectorusing thevectorcomponent of the view object. A pointer to a vector of typegsl_vector *orconst gsl_vector *can be obtained by taking the address of this component with the&operator.When using this pointer it is important to ensure that the view itself remains in scope—the simplest way to do so is by always writing the pointer as
&view.vector, and never storing this value in another variable.
-
gsl_vector_view gsl_vector_subvector(gsl_vector *v, size_t offset, size_t n)¶
-
gsl_vector_const_view gsl_vector_const_subvector(const gsl_vector *v, size_t offset, size_t n)¶
These functions return a vector view of a subvector of another vector
v. The start of the new vector is offset byoffsetelements from the start of the original vector. The new vector hasnelements. Mathematically, thei-th element of the new vectorv'is given by:v'(i) = v->data[(offset + i)*v->stride]
where the index
iruns from 0 ton - 1.The
datapointer of the returned vector struct is set to null if the combined parameters (offset,n) overrun the end of the original vector.The new vector is only a view of the block underlying the original vector,
v. The block containing the elements ofvis not owned by the new vector. When the view goes out of scope the original vectorvand its block will continue to exist. The original memory can only be deallocated by freeing the original vector. Of course, the original vector should not be deallocated while the view is still in use.The function
gsl_vector_const_subvector()is equivalent togsl_vector_subvector()but can be used for vectors which are declaredconst.
-
gsl_vector_view gsl_vector_subvector_with_stride(gsl_vector *v, size_t offset, size_t stride, size_t n)¶
-
gsl_vector_const_view gsl_vector_const_subvector_with_stride(const gsl_vector *v, size_t offset, size_t stride, size_t n)¶
These functions return a vector view of a subvector of another vector
vwith an additional stride argument. The subvector is formed in the same way as forgsl_vector_subvector()but the new vector hasnelements with a step-size ofstridefrom one element to the next in the original vector. Mathematically, thei-th element of the new vectorv'is given by:v'(i) = v->data[(offset + i*stride)*v->stride]
where the index
iruns from 0 ton - 1.Note that subvector views give direct access to the underlying elements of the original vector. For example, the following code will zero the even elements of the vector
vof lengthn, while leaving the odd elements untouched:gsl_vector_view v_even = gsl_vector_subvector_with_stride (v, 0, 2, n/2); gsl_vector_set_zero (&v_even.vector);
A vector view can be passed to any subroutine which takes a vector argument just as a directly allocated vector would be, using
&view.vector. For example, the following code computes the norm of the odd elements ofvusing the BLAS routinednrm2:gsl_vector_view v_odd = gsl_vector_subvector_with_stride (v, 1, 2, n/2); double r = gsl_blas_dnrm2 (&v_odd.vector);
The function
gsl_vector_const_subvector_with_stride()is equivalent togsl_vector_subvector_with_stride()but can be used for vectors which are declaredconst.
-
gsl_vector_view gsl_vector_complex_real(gsl_vector_complex *v)¶
-
gsl_vector_const_view gsl_vector_complex_const_real(const gsl_vector_complex *v)¶
These functions return a vector view of the real parts of the complex vector
v.The function
gsl_vector_complex_const_real()is equivalent togsl_vector_complex_real()but can be used for vectors which are declaredconst.
-
gsl_vector_view gsl_vector_complex_imag(gsl_vector_complex *v)¶
-
gsl_vector_const_view gsl_vector_complex_const_imag(const gsl_vector_complex *v)¶
These functions return a vector view of the imaginary parts of the complex vector
v.The function
gsl_vector_complex_const_imag()is equivalent togsl_vector_complex_imag()but can be used for vectors which are declaredconst.
-
gsl_vector_view gsl_vector_view_array(double *base, size_t n)¶
-
gsl_vector_const_view gsl_vector_const_view_array(const double *base, size_t n)¶
These functions return a vector view of an array. The start of the new vector is given by
baseand hasnelements. Mathematically, thei-th element of the new vectorv'is given by:v'(i) = base[i]
where the index
iruns from 0 ton - 1.The array containing the elements of
vis not owned by the new vector view. When the view goes out of scope the original array will continue to exist. The original memory can only be deallocated by freeing the original pointerbase. Of course, the original array should not be deallocated while the view is still in use.The function
gsl_vector_const_view_array()is equivalent togsl_vector_view_array()but can be used for arrays which are declaredconst.
-
gsl_vector_view gsl_vector_view_array_with_stride(double *base, size_t stride, size_t n)¶
-
gsl_vector_const_view gsl_vector_const_view_array_with_stride(const double *base, size_t stride, size_t n)¶
These functions return a vector view of an array
basewith an additional stride argument. The subvector is formed in the same way as forgsl_vector_view_array()but the new vector hasnelements with a step-size ofstridefrom one element to the next in the original array. Mathematically, thei-th element of the new vectorv'is given by:v'(i) = base[i*stride]
where the index
iruns from 0 ton - 1.Note that the view gives direct access to the underlying elements of the original array. A vector view can be passed to any subroutine which takes a vector argument just as a directly allocated vector would be, using
&view.vector.The function
gsl_vector_const_view_array_with_stride()is equivalent togsl_vector_view_array_with_stride()but can be used for arrays which are declaredconst.
Copying vectors¶
Common operations on vectors such as addition and multiplication are available in the BLAS part of the library (see BLAS Support). However, it is useful to have a small number of utility functions which do not require the full BLAS code. The following functions fall into this category.
-
int gsl_vector_memcpy(gsl_vector *dest, const gsl_vector *src)¶
This function copies the elements of the vector
srcinto the vectordest. The two vectors must have the same length.
-
int gsl_vector_complex_conj_memcpy(gsl_vector_complex *dest, const gsl_vector_complex *src)¶
This function copies the complex conjugate of the vector
srcinto the vectordest. The two vectors must have the same length.
-
int gsl_vector_swap(gsl_vector *v, gsl_vector *w)¶
This function exchanges the elements of the vectors
vandwby copying. The two vectors must have the same length.
Exchanging elements¶
The following functions can be used to exchange, or permute, the elements of a vector.
-
int gsl_vector_swap_elements(gsl_vector *v, size_t i, size_t j)¶
This function exchanges the
i-th andj-th elements of the vectorvin-place.
-
int gsl_vector_reverse(gsl_vector *v)¶
This function reverses the order of the elements of the vector
v.
Vector operations¶
-
int gsl_vector_add(gsl_vector *a, const gsl_vector *b)¶
This function adds the elements of vector
bto the elements of vectora. The result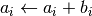 is stored
in
is stored
in aandbremains unchanged. The two vectors must have the same length.
-
int gsl_vector_sub(gsl_vector *a, const gsl_vector *b)¶
This function subtracts the elements of vector
bfrom the elements of vectora. The result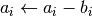 is stored
in
is stored
in aandbremains unchanged. The two vectors must have the same length.
-
int gsl_vector_mul(gsl_vector *a, const gsl_vector *b)¶
This function multiplies the elements of vector
aby the elements of vectorb. The result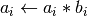 is stored in
is stored in aandbremains unchanged. The two vectors must have the same length.
-
int gsl_vector_div(gsl_vector *a, const gsl_vector *b)¶
This function divides the elements of vector
aby the elements of vectorb. The result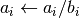 is
stored in
is
stored in aandbremains unchanged. The two vectors must have the same length.
-
int gsl_vector_scale(gsl_vector *a, const double x)¶
This function multiplies the elements of vector
aby the constant factorx. The result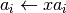 is
stored in
is
stored in a.
-
int gsl_vector_add_constant(gsl_vector *a, const double x)¶
This function adds the constant value
xto the elements of the vectora. The result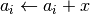 is stored in
is stored in
a.
-
double gsl_vector_sum(const gsl_vector *a)¶
This function returns the sum of the elements of
a, defined as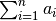
-
int gsl_vector_axpby(const double alpha, const gsl_vector *x, const double beta, gsl_vector *y)¶
This function performs the operation
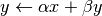 . The
vectors
. The
vectors xandymust have the same length.
The following additional functions are available for complex vector operations.
Finding maximum and minimum elements of vectors¶
The following operations are only defined for real vectors.
-
double gsl_vector_max(const gsl_vector *v)¶
This function returns the maximum value in the vector
v.
-
double gsl_vector_min(const gsl_vector *v)¶
This function returns the minimum value in the vector
v.
-
void gsl_vector_minmax(const gsl_vector *v, double *min_out, double *max_out)¶
This function returns the minimum and maximum values in the vector
v, storing them inmin_outandmax_out.
-
size_t gsl_vector_max_index(const gsl_vector *v)¶
This function returns the index of the maximum value in the vector
v. When there are several equal maximum elements then the lowest index is returned.
-
size_t gsl_vector_min_index(const gsl_vector *v)¶
This function returns the index of the minimum value in the vector
v. When there are several equal minimum elements then the lowest index is returned.
-
void gsl_vector_minmax_index(const gsl_vector *v, size_t *imin, size_t *imax)¶
This function returns the indices of the minimum and maximum values in the vector
v, storing them iniminandimax. When there are several equal minimum or maximum elements then the lowest indices are returned.
Vector properties¶
The following functions are defined for real and complex vectors. For complex vectors both the real and imaginary parts must satisfy the conditions.
-
int gsl_vector_isnull(const gsl_vector *v)¶
-
int gsl_vector_ispos(const gsl_vector *v)¶
-
int gsl_vector_isneg(const gsl_vector *v)¶
-
int gsl_vector_isnonneg(const gsl_vector *v)¶
These functions return 1 if all the elements of the vector
vare zero, strictly positive, strictly negative, or non-negative respectively, and 0 otherwise.
-
int gsl_vector_equal(const gsl_vector *u, const gsl_vector *v)¶
This function returns 1 if the vectors
uandvare equal (by comparison of element values) and 0 otherwise.
Example programs for vectors¶
This program shows how to allocate, initialize and read from a vector
using the functions gsl_vector_alloc(), gsl_vector_set() and
gsl_vector_get().
#include <stdio.h>
#include <gsl/gsl_vector.h>
int
main (void)
{
int i;
gsl_vector * v = gsl_vector_alloc (3);
for (i = 0; i < 3; i++)
{
gsl_vector_set (v, i, 1.23 + i);
}
for (i = 0; i < 100; i++) /* OUT OF RANGE ERROR */
{
printf ("v_%d = %g\n", i, gsl_vector_get (v, i));
}
gsl_vector_free (v);
return 0;
}
Here is the output from the program. The final loop attempts to read
outside the range of the vector v, and the error is trapped by
the range-checking code in gsl_vector_get().
$ ./a.out
v_0 = 1.23
v_1 = 2.23
v_2 = 3.23
gsl: vector_source.c:12: ERROR: index out of range
Default GSL error handler invoked.
Aborted (core dumped)
The next program shows how to write a vector to a file.
#include <stdio.h>
#include <gsl/gsl_vector.h>
int
main (void)
{
int i;
gsl_vector * v = gsl_vector_alloc (100);
for (i = 0; i < 100; i++)
{
gsl_vector_set (v, i, 1.23 + i);
}
{
FILE * f = fopen ("test.dat", "w");
gsl_vector_fprintf (f, v, "%.5g");
fclose (f);
}
gsl_vector_free (v);
return 0;
}
After running this program the file test.dat should contain the
elements of v, written using the format specifier
%.5g. The vector could then be read back in using the function
gsl_vector_fscanf (f, v) as follows:
#include <stdio.h>
#include <gsl/gsl_vector.h>
int
main (void)
{
int i;
gsl_vector * v = gsl_vector_alloc (10);
{
FILE * f = fopen ("test.dat", "r");
gsl_vector_fscanf (f, v);
fclose (f);
}
for (i = 0; i < 10; i++)
{
printf ("%g\n", gsl_vector_get(v, i));
}
gsl_vector_free (v);
return 0;
}
Matrices¶
Matrices are defined by a gsl_matrix structure which describes a
generalized slice of a block. Like a vector it represents a set of
elements in an area of memory, but uses two indices instead of one.
-
type gsl_matrix¶
The
gsl_matrixstructure contains six components, the two dimensions of the matrix, a physical dimension, a pointer to the memory where the elements of the matrix are stored,data, a pointer to the block owned by the matrixblock, if any, and an ownership flag,owner. The physical dimension determines the memory layout and can differ from the matrix dimension to allow the use of submatrices. Thegsl_matrixstructure is very simple and looks like this:typedef struct { size_t size1; size_t size2; size_t tda; double * data; gsl_block * block; int owner; } gsl_matrix;
Matrices are stored in row-major order, meaning that each row of
elements forms a contiguous block in memory. This is the standard
“C-language ordering” of two-dimensional arrays. Note that Fortran
stores arrays in column-major order. The number of rows is size1.
The range of valid row indices runs from 0 to size1 - 1. Similarly
size2 is the number of columns. The range of valid column indices
runs from 0 to size2 - 1. The physical row dimension tda, or
trailing dimension, specifies the size of a row of the matrix as
laid out in memory.
For example, in the following matrix size1 is 3, size2 is 4,
and tda is 8. The physical memory layout of the matrix begins in
the top left hand-corner and proceeds from left to right along each row
in turn.
00 01 02 03 XX XX XX XX
10 11 12 13 XX XX XX XX
20 21 22 23 XX XX XX XX
Each unused memory location is represented by “XX”. The
pointer data gives the location of the first element of the matrix
in memory. The pointer block stores the location of the memory
block in which the elements of the matrix are located (if any). If the
matrix owns this block then the owner field is set to one and the
block will be deallocated when the matrix is freed. If the matrix is
only a slice of a block owned by another object then the owner field is
zero and any underlying block will not be freed.
The functions for allocating and accessing matrices are defined in
gsl_matrix.h.
Matrix allocation¶
The functions for allocating memory to a matrix follow the style of
malloc and free. They also perform their own error
checking. If there is insufficient memory available to allocate a matrix
then the functions call the GSL error handler (with an error number of
GSL_ENOMEM) in addition to returning a null pointer. Thus if you
use the library error handler to abort your program then it isn’t
necessary to check every alloc.
-
gsl_matrix *gsl_matrix_alloc(size_t n1, size_t n2)¶
This function creates a matrix of size
n1rows byn2columns, returning a pointer to a newly initialized matrix struct. A new block is allocated for the elements of the matrix, and stored in theblockcomponent of the matrix struct. The block is “owned” by the matrix, and will be deallocated when the matrix is deallocated. Requesting zero forn1orn2is valid and returns a non-null result.
-
gsl_matrix *gsl_matrix_calloc(size_t n1, size_t n2)¶
This function allocates memory for a matrix of size
n1rows byn2columns and initializes all the elements of the matrix to zero.
-
void gsl_matrix_free(gsl_matrix *m)¶
This function frees a previously allocated matrix
m. If the matrix was created usinggsl_matrix_alloc()then the block underlying the matrix will also be deallocated. If the matrix has been created from another object then the memory is still owned by that object and will not be deallocated.
Accessing matrix elements¶
The functions for accessing the elements of a matrix use the same range
checking system as vectors. You can turn off range checking by recompiling
your program with the preprocessor definition
GSL_RANGE_CHECK_OFF.
The elements of the matrix are stored in “C-order”, where the second
index moves continuously through memory. More precisely, the element
accessed by the function gsl_matrix_get(m,i,j) and
gsl_matrix_set(m,i,j,x) is:
m->data[i * m->tda + j]
where tda is the physical row-length of the matrix.
-
double gsl_matrix_get(const gsl_matrix *m, const size_t i, const size_t j)¶
This function returns the
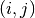 -th element of a matrix
-th element of a matrix
m. Ifiorjlie outside the allowed range of 0 ton1 - 1and 0 ton2 - 1then the error handler is invoked and 0 is returned. An inline version of this function is used whenHAVE_INLINEis defined.
-
void gsl_matrix_set(gsl_matrix *m, const size_t i, const size_t j, double x)¶
This function sets the value of the
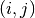 -th element of a
matrix
-th element of a
matrix mtox. Ifiorjlies outside the allowed range of 0 ton1 - 1and 0 ton2 - 1then the error handler is invoked. An inline version of this function is used whenHAVE_INLINEis defined.
-
double *gsl_matrix_ptr(gsl_matrix *m, size_t i, size_t j)¶
-
const double *gsl_matrix_const_ptr(const gsl_matrix *m, size_t i, size_t j)¶
These functions return a pointer to the
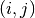 -th element of a
matrix
-th element of a
matrix m. Ifiorjlie outside the allowed range of 0 ton1 - 1and 0 ton2 - 1then the error handler is invoked and a null pointer is returned. Inline versions of these functions are used whenHAVE_INLINEis defined.
Initializing matrix elements¶
-
void gsl_matrix_set_all(gsl_matrix *m, double x)¶
This function sets all the elements of the matrix
mto the valuex.
-
void gsl_matrix_set_zero(gsl_matrix *m)¶
This function sets all the elements of the matrix
mto zero.
-
void gsl_matrix_set_identity(gsl_matrix *m)¶
This function sets the elements of the matrix
mto the corresponding elements of the identity matrix,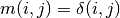 ,
i.e. a unit diagonal with all off-diagonal elements zero.
This applies to both square and rectangular matrices.
,
i.e. a unit diagonal with all off-diagonal elements zero.
This applies to both square and rectangular matrices.
Reading and writing matrices¶
The library provides functions for reading and writing matrices to a file as binary data or formatted text.
-
int gsl_matrix_fwrite(FILE *stream, const gsl_matrix *m)¶
This function writes the elements of the matrix
mto the streamstreamin binary format. The return value is 0 for success andGSL_EFAILEDif there was a problem writing to the file. Since the data is written in the native binary format it may not be portable between different architectures.
-
int gsl_matrix_fread(FILE *stream, gsl_matrix *m)¶
This function reads into the matrix
mfrom the open streamstreamin binary format. The matrixmmust be preallocated with the correct dimensions since the function uses the size ofmto determine how many bytes to read. The return value is 0 for success andGSL_EFAILEDif there was a problem reading from the file. The data is assumed to have been written in the native binary format on the same architecture.
-
int gsl_matrix_fprintf(FILE *stream, const gsl_matrix *m, const char *format)¶
This function writes the elements of the matrix
mline-by-line to the streamstreamusing the format specifierformat, which should be one of the%g,%eor%fformats for floating point numbers and%dfor integers. The function returns 0 for success andGSL_EFAILEDif there was a problem writing to the file.
-
int gsl_matrix_fscanf(FILE *stream, gsl_matrix *m)¶
This function reads formatted data from the stream
streaminto the matrixm. The matrixmmust be preallocated with the correct dimensions since the function uses the size ofmto determine how many numbers to read. The function returns 0 for success andGSL_EFAILEDif there was a problem reading from the file.
Matrix views¶
-
type gsl_matrix_view¶
-
type gsl_matrix_const_view¶
A matrix view is a temporary object, stored on the stack, which can be used to operate on a subset of matrix elements. Matrix views can be defined for both constant and non-constant matrices using separate types that preserve constness. A matrix view has the type
gsl_matrix_viewand a constant matrix view has the typegsl_matrix_const_view. In both cases the elements of the view can by accessed using thematrixcomponent of the view object. A pointergsl_matrix *orconst gsl_matrix *can be obtained by taking the address of thematrixcomponent with the&operator. In addition to matrix views it is also possible to create vector views of a matrix, such as row or column views.
-
gsl_matrix_view gsl_matrix_submatrix(gsl_matrix *m, size_t k1, size_t k2, size_t n1, size_t n2)¶
-
gsl_matrix_const_view gsl_matrix_const_submatrix(const gsl_matrix *m, size_t k1, size_t k2, size_t n1, size_t n2)¶
These functions return a matrix view of a submatrix of the matrix
m. The upper-left element of the submatrix is the element (k1,k2) of the original matrix. The submatrix hasn1rows andn2columns. The physical number of columns in memory given bytdais unchanged. Mathematically, the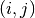 -th element of the new matrix is given by:
-th element of the new matrix is given by:m'(i,j) = m->data[(k1*m->tda + k2) + i*m->tda + j]
where the index
iruns from 0 ton1 - 1and the indexjruns from 0 ton2 - 1.The
datapointer of the returned matrix struct is set to null if the combined parameters (i,j,n1,n2,tda) overrun the ends of the original matrix.The new matrix view is only a view of the block underlying the existing matrix,
m. The block containing the elements ofmis not owned by the new matrix view. When the view goes out of scope the original matrixmand its block will continue to exist. The original memory can only be deallocated by freeing the original matrix. Of course, the original matrix should not be deallocated while the view is still in use.The function
gsl_matrix_const_submatrix()is equivalent togsl_matrix_submatrix()but can be used for matrices which are declaredconst.
-
gsl_matrix_view gsl_matrix_view_array(double *base, size_t n1, size_t n2)¶
-
gsl_matrix_const_view gsl_matrix_const_view_array(const double *base, size_t n1, size_t n2)¶
These functions return a matrix view of the array
base. The matrix hasn1rows andn2columns. The physical number of columns in memory is also given byn2. Mathematically, the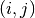 -th element of the new matrix is given by:
-th element of the new matrix is given by:m'(i,j) = base[i*n2 + j]
where the index
iruns from 0 ton1 - 1and the indexjruns from 0 ton2 - 1.The new matrix is only a view of the array
base. When the view goes out of scope the original arraybasewill continue to exist. The original memory can only be deallocated by freeing the original array. Of course, the original array should not be deallocated while the view is still in use.The function
gsl_matrix_const_view_array()is equivalent togsl_matrix_view_array()but can be used for matrices which are declaredconst.
-
gsl_matrix_view gsl_matrix_view_array_with_tda(double *base, size_t n1, size_t n2, size_t tda)¶
-
gsl_matrix_const_view gsl_matrix_const_view_array_with_tda(const double *base, size_t n1, size_t n2, size_t tda)¶
These functions return a matrix view of the array
basewith a physical number of columnstdawhich may differ from the corresponding dimension of the matrix. The matrix hasn1rows andn2columns, and the physical number of columns in memory is given bytda. Mathematically, the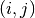 -th element of the new
matrix is given by:
-th element of the new
matrix is given by:m'(i,j) = base[i*tda + j]
where the index
iruns from 0 ton1 - 1and the indexjruns from 0 ton2 - 1.The new matrix is only a view of the array
base. When the view goes out of scope the original arraybasewill continue to exist. The original memory can only be deallocated by freeing the original array. Of course, the original array should not be deallocated while the view is still in use.The function
gsl_matrix_const_view_array_with_tda()is equivalent togsl_matrix_view_array_with_tda()but can be used for matrices which are declaredconst.
-
gsl_matrix_view gsl_matrix_view_vector(gsl_vector *v, size_t n1, size_t n2)¶
-
gsl_matrix_const_view gsl_matrix_const_view_vector(const gsl_vector *v, size_t n1, size_t n2)¶
These functions return a matrix view of the vector
v. The matrix hasn1rows andn2columns. The vector must have unit stride. The physical number of columns in memory is also given byn2. Mathematically, the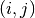 -th element of the new
matrix is given by:
-th element of the new
matrix is given by:m'(i,j) = v->data[i*n2 + j]
where the index
iruns from 0 ton1 - 1and the indexjruns from 0 ton2 - 1.The new matrix is only a view of the vector
v. When the view goes out of scope the original vectorvwill continue to exist. The original memory can only be deallocated by freeing the original vector. Of course, the original vector should not be deallocated while the view is still in use.The function
gsl_matrix_const_view_vector()is equivalent togsl_matrix_view_vector()but can be used for matrices which are declaredconst.
-
gsl_matrix_view gsl_matrix_view_vector_with_tda(gsl_vector *v, size_t n1, size_t n2, size_t tda)¶
-
gsl_matrix_const_view gsl_matrix_const_view_vector_with_tda(const gsl_vector *v, size_t n1, size_t n2, size_t tda)¶
These functions return a matrix view of the vector
vwith a physical number of columnstdawhich may differ from the corresponding matrix dimension. The vector must have unit stride. The matrix hasn1rows andn2columns, and the physical number of columns in memory is given bytda. Mathematically, the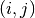 -th element of the new matrix is given by:
-th element of the new matrix is given by:m'(i,j) = v->data[i*tda + j]
where the index
iruns from 0 ton1 - 1and the indexjruns from 0 ton2 - 1.The new matrix is only a view of the vector
v. When the view goes out of scope the original vectorvwill continue to exist. The original memory can only be deallocated by freeing the original vector. Of course, the original vector should not be deallocated while the view is still in use.The function
gsl_matrix_const_view_vector_with_tda()is equivalent togsl_matrix_view_vector_with_tda()but can be used for matrices which are declaredconst.
Creating row and column views¶
In general there are two ways to access an object, by reference or by copying. The functions described in this section create vector views which allow access to a row or column of a matrix by reference. Modifying elements of the view is equivalent to modifying the matrix, since both the vector view and the matrix point to the same memory block.
-
gsl_vector_view gsl_matrix_row(gsl_matrix *m, size_t i)¶
-
gsl_vector_const_view gsl_matrix_const_row(const gsl_matrix *m, size_t i)¶
These functions return a vector view of the
i-th row of the matrixm. Thedatapointer of the new vector is set to null ifiis out of range.The function
gsl_matrix_const_row()is equivalent togsl_matrix_row()but can be used for matrices which are declaredconst.
-
gsl_vector_view gsl_matrix_column(gsl_matrix *m, size_t j)¶
-
gsl_vector_const_view gsl_matrix_const_column(const gsl_matrix *m, size_t j)¶
These functions return a vector view of the
j-th column of the matrixm. Thedatapointer of the new vector is set to null ifjis out of range.The function
gsl_matrix_const_column()is equivalent togsl_matrix_column()but can be used for matrices which are declaredconst.
-
gsl_vector_view gsl_matrix_subrow(gsl_matrix *m, size_t i, size_t offset, size_t n)¶
-
gsl_vector_const_view gsl_matrix_const_subrow(const gsl_matrix *m, size_t i, size_t offset, size_t n)¶
These functions return a vector view of the
i-th row of the matrixmbeginning atoffsetelements past the first column and containingnelements. Thedatapointer of the new vector is set to null ifi,offset, ornare out of range.The function
gsl_matrix_const_subrow()is equivalent togsl_matrix_subrow()but can be used for matrices which are declaredconst.
-
gsl_vector_view gsl_matrix_subcolumn(gsl_matrix *m, size_t j, size_t offset, size_t n)¶
-
gsl_vector_const_view gsl_matrix_const_subcolumn(const gsl_matrix *m, size_t j, size_t offset, size_t n)¶
These functions return a vector view of the
j-th column of the matrixmbeginning atoffsetelements past the first row and containingnelements. Thedatapointer of the new vector is set to null ifj,offset, ornare out of range.The function
gsl_matrix_const_subcolumn()is equivalent togsl_matrix_subcolumn()but can be used for matrices which are declaredconst.
-
gsl_vector_view gsl_matrix_diagonal(gsl_matrix *m)¶
-
gsl_vector_const_view gsl_matrix_const_diagonal(const gsl_matrix *m)¶
These functions return a vector view of the diagonal of the matrix
m. The matrixmis not required to be square. For a rectangular matrix the length of the diagonal is the same as the smaller dimension of the matrix.The function
gsl_matrix_const_diagonal()is equivalent togsl_matrix_diagonal()but can be used for matrices which are declaredconst.
-
gsl_vector_view gsl_matrix_subdiagonal(gsl_matrix *m, size_t k)¶
-
gsl_vector_const_view gsl_matrix_const_subdiagonal(const gsl_matrix *m, size_t k)¶
These functions return a vector view of the
k-th subdiagonal of the matrixm. The matrixmis not required to be square. The diagonal of the matrix corresponds to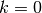 .
.The function
gsl_matrix_const_subdiagonal()is equivalent togsl_matrix_subdiagonal()but can be used for matrices which are declaredconst.
-
gsl_vector_view gsl_matrix_superdiagonal(gsl_matrix *m, size_t k)¶
-
gsl_vector_const_view gsl_matrix_const_superdiagonal(const gsl_matrix *m, size_t k)¶
These functions return a vector view of the
k-th superdiagonal of the matrixm. The matrixmis not required to be square. The diagonal of the matrix corresponds to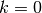 .
.The function
gsl_matrix_const_superdiagonal()is equivalent togsl_matrix_superdiagonal()but can be used for matrices which are declaredconst.
Copying matrices¶
-
int gsl_matrix_memcpy(gsl_matrix *dest, const gsl_matrix *src)¶
This function copies the elements of the matrix
srcinto the matrixdest. The two matrices must have the same size.
-
int gsl_matrix_swap(gsl_matrix *m1, gsl_matrix *m2)¶
This function exchanges the elements of the matrices
m1andm2by copying. The two matrices must have the same size.
Copying rows and columns¶
The functions described in this section copy a row or column of a matrix
into a vector. This allows the elements of the vector and the matrix to
be modified independently. Note that if the matrix and the vector point
to overlapping regions of memory then the result will be undefined. The
same effect can be achieved with more generality using
gsl_vector_memcpy() with vector views of rows and columns.
-
int gsl_matrix_get_row(gsl_vector *v, const gsl_matrix *m, size_t i)¶
This function copies the elements of the
i-th row of the matrixminto the vectorv. The length of the vector must be the same as the length of the row.
-
int gsl_matrix_get_col(gsl_vector *v, const gsl_matrix *m, size_t j)¶
This function copies the elements of the
j-th column of the matrixminto the vectorv. The length of the vector must be the same as the length of the column.
-
int gsl_matrix_set_row(gsl_matrix *m, size_t i, const gsl_vector *v)¶
This function copies the elements of the vector
vinto thei-th row of the matrixm. The length of the vector must be the same as the length of the row.
-
int gsl_matrix_set_col(gsl_matrix *m, size_t j, const gsl_vector *v)¶
This function copies the elements of the vector
vinto thej-th column of the matrixm. The length of the vector must be the same as the length of the column.
Exchanging rows and columns¶
The following functions can be used to exchange the rows and columns of a matrix.
-
int gsl_matrix_swap_rows(gsl_matrix *m, size_t i, size_t j)¶
This function exchanges the
i-th andj-th rows of the matrixmin-place.
-
int gsl_matrix_swap_columns(gsl_matrix *m, size_t i, size_t j)¶
This function exchanges the
i-th andj-th columns of the matrixmin-place.
-
int gsl_matrix_swap_rowcol(gsl_matrix *m, size_t i, size_t j)¶
This function exchanges the
i-th row andj-th column of the matrixmin-place. The matrix must be square for this operation to be possible.
-
int gsl_matrix_transpose_memcpy(gsl_matrix *dest, const gsl_matrix *src)¶
This function makes the matrix
destthe transpose of the matrixsrcby copying the elements ofsrcintodest. This function works for all matrices provided that the dimensions of the matrixdestmatch the transposed dimensions of the matrixsrc.
-
int gsl_matrix_transpose(gsl_matrix *m)¶
This function replaces the matrix
mby its transpose by copying the elements of the matrix in-place. The matrix must be square for this operation to be possible.
-
int gsl_matrix_complex_conjtrans_memcpy(gsl_matrix_complex *dest, const gsl_matrix_complex *src)¶
This function makes the matrix
destthe conjugate transpose of the matrixsrcby copying the complex conjugate elements ofsrcintodest. This function works for all complex matrices provided that the dimensions of the matrixdestmatch the transposed dimensions of the matrixsrc.
Matrix operations¶
The following operations are defined for real and complex matrices.
-
int gsl_matrix_add(gsl_matrix *a, const gsl_matrix *b)¶
This function adds the elements of matrix
bto the elements of matrixa. The result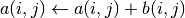 is stored in
is stored in aandbremains unchanged. The two matrices must have the same dimensions.
-
int gsl_matrix_sub(gsl_matrix *a, const gsl_matrix *b)¶
This function subtracts the elements of matrix
bfrom the elements of matrixa. The result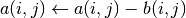 is stored in
is stored in aandbremains unchanged. The two matrices must have the same dimensions.
-
int gsl_matrix_mul_elements(gsl_matrix *a, const gsl_matrix *b)¶
This function multiplies the elements of matrix
aby the elements of matrixb. The result is stored in
is stored in aandbremains unchanged. The two matrices must have the same dimensions.
-
int gsl_matrix_div_elements(gsl_matrix *a, const gsl_matrix *b)¶
This function divides the elements of matrix
aby the elements of matrixb. The result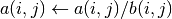 is stored in
is stored in aandbremains unchanged. The two matrices must have the same dimensions.
-
int gsl_matrix_scale(gsl_matrix *a, const double x)¶
This function multiplies the elements of matrix
aby the constant factorx. The result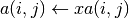 is stored in
is stored in a.
-
int gsl_matrix_scale_columns(gsl_matrix *A, const gsl_vector *x)¶
This function scales the columns of the
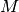 -by-
-by-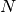 matrix
matrix
Aby the elements of the vectorx, of length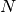 . The
. The
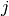 -th column of
-th column of Ais multiplied by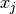 . This is equivalent to
forming
. This is equivalent to
forming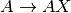
where
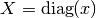 .
.
-
int gsl_matrix_scale_rows(gsl_matrix *A, const gsl_vector *x)¶
This function scales the rows of the
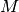 -by-
-by-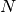 matrix
matrix
Aby the elements of the vectorx, of length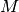 . The
. The
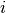 -th row of
-th row of Ais multiplied by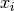 . This is equivalent to
forming
. This is equivalent to
forming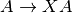
where
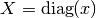 .
.
-
int gsl_matrix_add_constant(gsl_matrix *a, const double x)¶
This function adds the constant value
xto the elements of the matrixa. The result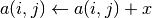 is
stored in
is
stored in a.
-
int gsl_matrix_complex_conjugate(gsl_matrix *a)¶
This function replaces each element of the matrix
awith its complex conjugate value. The result is stored in
is stored in a.
Finding maximum and minimum elements of matrices¶
The following operations are only defined for real matrices.
-
double gsl_matrix_max(const gsl_matrix *m)¶
This function returns the maximum value in the matrix
m.
-
double gsl_matrix_min(const gsl_matrix *m)¶
This function returns the minimum value in the matrix
m.
-
void gsl_matrix_minmax(const gsl_matrix *m, double *min_out, double *max_out)¶
This function returns the minimum and maximum values in the matrix
m, storing them inmin_outandmax_out.
-
void gsl_matrix_max_index(const gsl_matrix *m, size_t *imax, size_t *jmax)¶
This function returns the indices of the maximum value in the matrix
m, storing them inimaxandjmax. When there are several equal maximum elements then the first element found is returned, searching in row-major order.
-
void gsl_matrix_min_index(const gsl_matrix *m, size_t *imin, size_t *jmin)¶
This function returns the indices of the minimum value in the matrix
m, storing them iniminandjmin. When there are several equal minimum elements then the first element found is returned, searching in row-major order.
-
void gsl_matrix_minmax_index(const gsl_matrix *m, size_t *imin, size_t *jmin, size_t *imax, size_t *jmax)¶
This function returns the indices of the minimum and maximum values in the matrix
m, storing them in (imin,jmin) and (imax,jmax). When there are several equal minimum or maximum elements then the first elements found are returned, searching in row-major order.
Matrix properties¶
The following functions are defined for real and complex matrices. For complex matrices both the real and imaginary parts must satisfy the conditions.
-
int gsl_matrix_isnull(const gsl_matrix *m)¶
-
int gsl_matrix_ispos(const gsl_matrix *m)¶
-
int gsl_matrix_isneg(const gsl_matrix *m)¶
-
int gsl_matrix_isnonneg(const gsl_matrix *m)¶
These functions return 1 if all the elements of the matrix
mare zero, strictly positive, strictly negative, or non-negative respectively, and 0 otherwise. To test whether a matrix is positive-definite, use the Cholesky decomposition.
-
int gsl_matrix_equal(const gsl_matrix *a, const gsl_matrix *b)¶
This function returns 1 if the matrices
aandbare equal (by comparison of element values) and 0 otherwise.
-
double gsl_matrix_norm1(const gsl_matrix *A)¶
This function returns the 1-norm of the
 -by-
-by- matrix
matrix A, defined as the maximum column sum,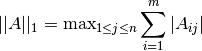
Example programs for matrices¶
The program below shows how to allocate, initialize and read from a matrix
using the functions gsl_matrix_alloc(), gsl_matrix_set() and
gsl_matrix_get().
#include <stdio.h>
#include <gsl/gsl_matrix.h>
int
main (void)
{
int i, j;
gsl_matrix * m = gsl_matrix_alloc (10, 3);
for (i = 0; i < 10; i++)
for (j = 0; j < 3; j++)
gsl_matrix_set (m, i, j, 0.23 + 100*i + j);
for (i = 0; i < 100; i++) /* OUT OF RANGE ERROR */
for (j = 0; j < 3; j++)
printf ("m(%d,%d) = %g\n", i, j,
gsl_matrix_get (m, i, j));
gsl_matrix_free (m);
return 0;
}
Here is the output from the program. The final loop attempts to read
outside the range of the matrix m, and the error is trapped by
the range-checking code in gsl_matrix_get().
$ ./a.out
m(0,0) = 0.23
m(0,1) = 1.23
m(0,2) = 2.23
m(1,0) = 100.23
m(1,1) = 101.23
m(1,2) = 102.23
...
m(9,2) = 902.23
gsl: matrix_source.c:13: ERROR: first index out of range
Default GSL error handler invoked.
Aborted (core dumped)
The next program shows how to write a matrix to a file.
#include <stdio.h>
#include <gsl/gsl_matrix.h>
int
main (void)
{
int i, j, k = 0;
gsl_matrix * m = gsl_matrix_alloc (100, 100);
gsl_matrix * a = gsl_matrix_alloc (100, 100);
for (i = 0; i < 100; i++)
for (j = 0; j < 100; j++)
gsl_matrix_set (m, i, j, 0.23 + i + j);
{
FILE * f = fopen ("test.dat", "wb");
gsl_matrix_fwrite (f, m);
fclose (f);
}
{
FILE * f = fopen ("test.dat", "rb");
gsl_matrix_fread (f, a);
fclose (f);
}
for (i = 0; i < 100; i++)
for (j = 0; j < 100; j++)
{
double mij = gsl_matrix_get (m, i, j);
double aij = gsl_matrix_get (a, i, j);
if (mij != aij) k++;
}
gsl_matrix_free (m);
gsl_matrix_free (a);
printf ("differences = %d (should be zero)\n", k);
return (k > 0);
}
After running this program the file test.dat should contain the
elements of m, written in binary format. The matrix which is read
back in using the function gsl_matrix_fread() should be exactly
equal to the original matrix.
The following program demonstrates the use of vector views. The program computes the column norms of a matrix.
#include <math.h>
#include <stdio.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_blas.h>
int
main (void)
{
size_t i,j;
gsl_matrix *m = gsl_matrix_alloc (10, 10);
for (i = 0; i < 10; i++)
for (j = 0; j < 10; j++)
gsl_matrix_set (m, i, j, sin (i) + cos (j));
for (j = 0; j < 10; j++)
{
gsl_vector_view column = gsl_matrix_column (m, j);
double d;
d = gsl_blas_dnrm2 (&column.vector);
printf ("matrix column %zu, norm = %g\n", j, d);
}
gsl_matrix_free (m);
return 0;
}
Here is the output of the program,
matrix column 0, norm = 4.31461
matrix column 1, norm = 3.1205
matrix column 2, norm = 2.19316
matrix column 3, norm = 3.26114
matrix column 4, norm = 2.53416
matrix column 5, norm = 2.57281
matrix column 6, norm = 4.20469
matrix column 7, norm = 3.65202
matrix column 8, norm = 2.08524
matrix column 9, norm = 3.07313
The results can be confirmed using GNU octave:
$ octave
GNU Octave, version 2.0.16.92
octave> m = sin(0:9)' * ones(1,10)
+ ones(10,1) * cos(0:9);
octave> sqrt(sum(m.^2))
ans =
4.3146 3.1205 2.1932 3.2611 2.5342 2.5728
4.2047 3.6520 2.0852 3.0731
References and Further Reading¶
The block, vector and matrix objects in GSL follow the valarray
model of C++. A description of this model can be found in the following
reference,
B. Stroustrup, The C++ Programming Language (3rd Ed), Section 22.4 Vector Arithmetic. Addison-Wesley 1997, ISBN 0-201-88954-4.
Footnotes
- 1
Range checking is available in the GNU C Compiler bounds-checking extension, but it is not part of the default installation of GCC. Memory accesses can also be checked with Valgrind or the
gcc -fmudflapmemory protection option.