Quasi-Random Sequences

This chapter describes functions for generating quasi-random sequences in arbitrary dimensions. A quasi-random sequence progressively covers a 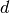-dimensional space with a set of points that are uniformly distributed. Quasi-random sequences are also known as low-discrepancy sequences. The quasi-random sequence generators use an interface that is similar to the interface for random number generators, except that seeding is not required—each generator produces a single sequence.

The functions described in this section are declared in the header file gsl_qrng.h.

Quasi-random number generator initialization

type gsl_qrng

This is a workspace for computing quasi-random sequences.

gsl_qrng *gsl_qrng_alloc(const gsl_qrng_type *T, unsigned int d)

This function returns a pointer to a newly-created instance of a quasi-random sequence generator of type T and dimension d. If there is insufficient memory to create the generator then the function returns a null pointer and the error handler is invoked with an error code of GSL_ENOMEM.

void gsl_qrng_free(gsl_qrng *q)

This function frees all the memory associated with the generator q.

void gsl_qrng_init(gsl_qrng *q)

This function reinitializes the generator q to its starting point. Note that quasi-random sequences do not use a seed and always produce the same set of values.

Sampling from a quasi-random number generator

int gsl_qrng_get(const gsl_qrng *q, double x[])

This function stores the next point from the sequence generator q in the array x. The space available for x must match the dimension of the generator. The point x will lie in the range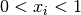 for each 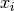. An inline version of this function is used when HAVE_INLINE is defined.

Auxiliary quasi-random number generator functions

const char *gsl_qrng_name(const gsl_qrng *q)

This function returns a pointer to the name of the generator.

size_t gsl_qrng_size(const gsl_qrng *q)

void *gsl_qrng_state(const gsl_qrng *q)

These functions return a pointer to the state of generator r and its size. You can use this information to access the state directly. For example, the following code will write the state of a generator to a stream:

void * state = gsl_qrng_state (q);
size_t n = gsl_qrng_size (q);
fwrite (state, n, 1, stream);

Saving and restoring quasi-random number generator state

int gsl_qrng_memcpy(gsl_qrng *dest, const gsl_qrng *src)

This function copies the quasi-random sequence generator src into the pre-existing generator dest, making dest into an exact copy of src. The two generators must be of the same type.

gsl_qrng *gsl_qrng_clone(const gsl_qrng *q)

This function returns a pointer to a newly created generator which is an exact copy of the generator q.

Quasi-random number generator algorithms

The following quasi-random sequence algorithms are available,

type gsl_qrng_type

gsl_qrng_type *gsl_qrng_niederreiter_2

This generator uses the algorithm described in Bratley, Fox, Niederreiter, ACM Trans. Model. Comp. Sim. 2, 195 (1992). It is valid up to 12 dimensions.

gsl_qrng_type *gsl_qrng_sobol

This generator uses the Sobol sequence described in Antonov, Saleev, USSR Comput. Maths. Math. Phys. 19, 252 (1980). It is valid up to 40 dimensions.

gsl_qrng_type *gsl_qrng_halton

gsl_qrng_type *gsl_qrng_reversehalton

These generators use the Halton and reverse Halton sequences described in J.H. Halton, Numerische Mathematik, 2, 84-90 (1960) and B. Vandewoestyne and R. Cools Computational and Applied Mathematics, 189, 1&2, 341-361 (2006). They are valid up to 1229 dimensions.

Examples

The following program prints the first 1024 points of the 2-dimensional Sobol sequence.

#include <stdio.h>
#include <gsl/gsl_qrng.h>

int
main (void)
{
  int i;
  gsl_qrng * q = gsl_qrng_alloc (gsl_qrng_sobol, 2);

  for (i = 0; i < 1024; i++)
    {
      double v[2];
      gsl_qrng_get (q, v);
      printf ("%.5f %.5f\n", v[0], v[1]);
    }

  gsl_qrng_free (q);
  return 0;
}

Here is the output from the program:

$ ./a.out
0.50000 0.50000
0.75000 0.25000
0.25000 0.75000
0.37500 0.37500
0.87500 0.87500
0.62500 0.12500
0.12500 0.62500
....

It can be seen that successive points progressively fill-in the spaces between previous points.

Fig. 4 shows the distribution in the x-y plane of the first 1024 points from the Sobol sequence,

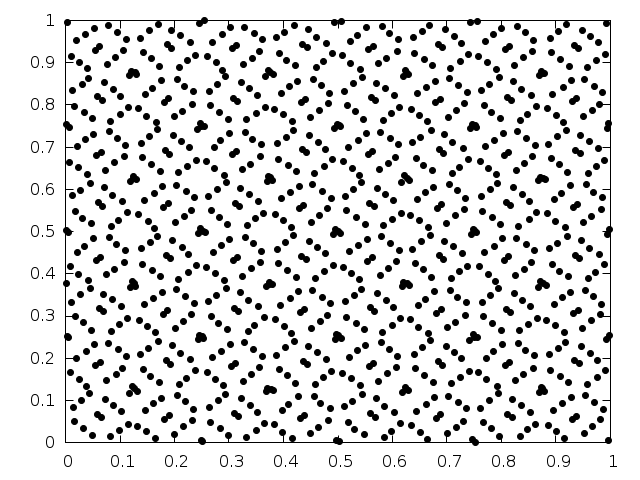
Fig. 4 Distribution of the first 1024 points from the quasi-random Sobol sequence

References

The implementations of the quasi-random sequence routines are based on the algorithms described in the following paper,

• P. Bratley and B.L. Fox and H. Niederreiter, “Algorithm 738: Programs to Generate Niederreiter’s Low-discrepancy Sequences”, ACM Transactions on Mathematical Software, Vol.: 20, No.: 4, December, 1994, p.: 494–495.