Ordinary Differential Equations¶
This chapter describes functions for solving ordinary differential equation (ODE) initial value problems. The library provides a variety of low-level methods, such as Runge-Kutta and Bulirsch-Stoer routines, and higher-level components for adaptive step-size control. The components can be combined by the user to achieve the desired solution, with full access to any intermediate steps. A driver object can be used as a high level wrapper for easy use of low level functions.
These functions are declared in the header file gsl_odeiv2.h.
This is a new interface in version 1.15 and uses the prefix
gsl_odeiv2 for all functions. It is recommended over the
previous gsl_odeiv implementation defined in gsl_odeiv.h
The old interface has been retained under the original name for
backwards compatibility.
Defining the ODE System¶
The routines solve the general 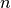 -dimensional first-order system,
-dimensional first-order system,
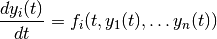
for 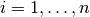 . The stepping functions rely on the vector
of derivatives
. The stepping functions rely on the vector
of derivatives 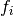 and the Jacobian matrix,
and the Jacobian matrix,
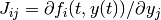
A system of equations is defined using the gsl_odeiv2_system
datatype.
-
type gsl_odeiv2_system¶
This data type defines a general ODE system with arbitrary parameters.
int (* function) (double t, const double y[], double dydt[], void * params)This function should store the vector elements
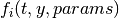 in the array
in the array dydt, for arguments (t,y) and parametersparams.The function should return
GSL_SUCCESSif the calculation was completed successfully. Any other return value indicates an error. A special return valueGSL_EBADFUNCcausesgsl_odeiv2routines to immediately stop and return. Iffunctionis modified (for example contents ofparams), the user must call an appropriate reset function (gsl_odeiv2_driver_reset(),gsl_odeiv2_evolve_reset()orgsl_odeiv2_step_reset()) before continuing. Use return values distinct from standard GSL error codes to distinguish your function as the source of the error.int (* jacobian) (double t, const double y[], double * dfdy, double dfdt[], void * params)This function should store the vector of derivative elements
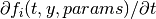
in the array
dfdtand the Jacobian matrix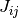 in the array
in the array dfdy, regarded as a row-ordered matrixJ(i,j) = dfdy[i * dimension + j]wheredimensionis the dimension of the system.Not all of the stepper algorithms of
gsl_odeiv2make use of the Jacobian matrix, so it may not be necessary to provide this function (thejacobianelement of the struct can be replaced by a null pointer for those algorithms).The function should return
GSL_SUCCESSif the calculation was completed successfully. Any other return value indicates an error. A special return valueGSL_EBADFUNCcausesgsl_odeiv2routines to immediately stop and return. Ifjacobianis modified (for example contents ofparams), the user must call an appropriate reset function (gsl_odeiv2_driver_reset(),gsl_odeiv2_evolve_reset()orgsl_odeiv2_step_reset()) before continuing. Use return values distinct from standard GSL error codes to distinguish your function as the source of the error.size_t dimensionThis is the dimension of the system of equations.
void * paramsThis is a pointer to the arbitrary parameters of the system.
Stepping Functions¶
The lowest level components are the stepping functions which
advance a solution from time 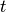 to
to 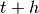 for a fixed
step-size
for a fixed
step-size 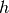 and estimate the resulting local error.
and estimate the resulting local error.
-
type gsl_odeiv2_step¶
This contains internal parameters for a stepping function.
-
gsl_odeiv2_step *gsl_odeiv2_step_alloc(const gsl_odeiv2_step_type *T, size_t dim)¶
This function returns a pointer to a newly allocated instance of a stepping function of type
Tfor a system ofdimdimensions. Please note that if you use a stepper method that requires access to a driver object, it is advisable to use a driver allocation method, which automatically allocates a stepper, too.
-
int gsl_odeiv2_step_reset(gsl_odeiv2_step *s)¶
This function resets the stepping function
s. It should be used whenever the next use ofswill not be a continuation of a previous step.
-
void gsl_odeiv2_step_free(gsl_odeiv2_step *s)¶
This function frees all the memory associated with the stepping function
s.
-
const char *gsl_odeiv2_step_name(const gsl_odeiv2_step *s)¶
This function returns a pointer to the name of the stepping function. For example:
printf ("step method is '%s'\n", gsl_odeiv2_step_name (s));
would print something like
step method is 'rkf45'.
-
unsigned int gsl_odeiv2_step_order(const gsl_odeiv2_step *s)¶
This function returns the order of the stepping function on the previous step. The order can vary if the stepping function itself is adaptive.
-
int gsl_odeiv2_step_set_driver(gsl_odeiv2_step *s, const gsl_odeiv2_driver *d)¶
This function sets a pointer of the driver object
dfor steppers, to allow the stepper to access control (and evolve) object through the driver object. This is a requirement for some steppers, to get the desired error level for internal iteration of stepper. Allocation of a driver object calls this function automatically.
-
int gsl_odeiv2_step_apply(gsl_odeiv2_step *s, double t, double h, double y[], double yerr[], const double dydt_in[], double dydt_out[], const gsl_odeiv2_system *sys)¶
This function applies the stepping function
sto the system of equations defined bysys, using the step-sizehto advance the system from timetand stateyto timet+h. The new state of the system is stored inyon output, with an estimate of the absolute error in each component stored inyerr. If the argumentdydt_inis not null it should point an array containing the derivatives for the system at timeton input. This is optional as the derivatives will be computed internally if they are not provided, but allows the reuse of existing derivative information. On output the new derivatives of the system at timet+hwill be stored indydt_outif it is not null.The stepping function returns
GSL_FAILUREif it is unable to compute the requested step. Also, if the user-supplied functions defined in the systemsysreturn a status other thanGSL_SUCCESSthe step will be aborted. In that case, the elements ofywill be restored to their pre-step values and the error code from the user-supplied function will be returned. Failure may be due to a singularity in the system or too large step-sizeh. In that case the step should be attempted again with a smaller step-size, e.g.h/ 2.If the driver object is not appropriately set via
gsl_odeiv2_step_set_driver()for those steppers that need it, the stepping function returnsGSL_EFAULT. If the user-supplied functions defined in the systemsysreturnsGSL_EBADFUNC, the function returns immediately with the same return code. In this case the user must callgsl_odeiv2_step_reset()before calling this function again.
The following algorithms are available. Please note that algorithms
which use step doubling for error estimation apply the more accurate
values from two half steps instead of values from a single step for
the new state y.
-
type gsl_odeiv2_step_type¶
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rk2¶
Explicit embedded Runge-Kutta (2, 3) method.
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rk4¶
Explicit 4th order (classical) Runge-Kutta. Error estimation is carried out by the step doubling method. For more efficient estimate of the error, use the embedded methods described below.
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rkf45¶
Explicit embedded Runge-Kutta-Fehlberg (4, 5) method. This method is a good general-purpose integrator.
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rkck¶
Explicit embedded Runge-Kutta Cash-Karp (4, 5) method.
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rk8pd¶
Explicit embedded Runge-Kutta Prince-Dormand (8, 9) method.
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rk1imp¶
Implicit Gaussian first order Runge-Kutta. Also known as implicit Euler or backward Euler method. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian and access to the driver object via
gsl_odeiv2_step_set_driver().
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rk2imp¶
Implicit Gaussian second order Runge-Kutta. Also known as implicit mid-point rule. Error estimation is carried out by the step doubling method. This stepper requires the Jacobian and access to the driver object via
gsl_odeiv2_step_set_driver().
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rk4imp¶
Implicit Gaussian 4th order Runge-Kutta. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian and access to the driver object via
gsl_odeiv2_step_set_driver().
-
gsl_odeiv2_step_type *gsl_odeiv2_step_bsimp¶
Implicit Bulirsch-Stoer method of Bader and Deuflhard. The method is generally suitable for stiff problems. This stepper requires the Jacobian.
-
gsl_odeiv2_step_type *gsl_odeiv2_step_msadams¶
A variable-coefficient linear multistep Adams method in Nordsieck form. This stepper uses explicit Adams-Bashforth (predictor) and implicit Adams-Moulton (corrector) methods in
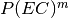 functional iteration mode. Method order varies dynamically between 1
and 12. This stepper requires the access to the driver object via
functional iteration mode. Method order varies dynamically between 1
and 12. This stepper requires the access to the driver object via
gsl_odeiv2_step_set_driver().
-
gsl_odeiv2_step_type *gsl_odeiv2_step_msbdf¶
A variable-coefficient linear multistep backward differentiation formula (BDF) method in Nordsieck form. This stepper uses the explicit BDF formula as predictor and implicit BDF formula as corrector. A modified Newton iteration method is used to solve the system of non-linear equations. Method order varies dynamically between 1 and 5. The method is generally suitable for stiff problems. This stepper requires the Jacobian and the access to the driver object via
gsl_odeiv2_step_set_driver().
-
gsl_odeiv2_step_type *gsl_odeiv2_step_rk2¶
Adaptive Step-size Control¶
The control function examines the proposed change to the solution produced by a stepping function and attempts to determine the optimal step-size for a user-specified level of error.
-
type gsl_odeiv2_control¶
This is a workspace for controlling step size.
-
type gsl_odeiv2_control_type¶
This specifies the control type.
-
gsl_odeiv2_control *gsl_odeiv2_control_standard_new(double eps_abs, double eps_rel, double a_y, double a_dydt)¶
The standard control object is a four parameter heuristic based on absolute and relative errors
eps_absandeps_rel, and scaling factorsa_yanda_dydtfor the system state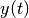 and derivatives
and derivatives 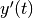 respectively.
respectively.The step-size adjustment procedure for this method begins by computing the desired error level
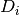 for each component,
for each component,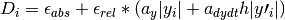
and comparing it with the observed error
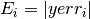 . If the
observed error
. If the
observed error Eexceeds the desired error levelDby more than 10% for any component then the method reduces the step-size by an appropriate factor,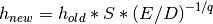
where
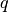 is the consistency order of the method (e.g.
is the consistency order of the method (e.g. 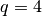 for
4(5) embedded RK), and
for
4(5) embedded RK), and 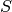 is a safety factor of 0.9. The ratio
is a safety factor of 0.9. The ratio
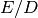 is taken to be the maximum of the ratios
is taken to be the maximum of the ratios
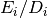 .
.If the observed error
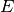 is less than 50% of the desired error
level
is less than 50% of the desired error
level Dfor the maximum ratio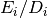 then the algorithm
takes the opportunity to increase the step-size to bring the error in
line with the desired level,
then the algorithm
takes the opportunity to increase the step-size to bring the error in
line with the desired level,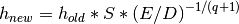
This encompasses all the standard error scaling methods. To avoid uncontrolled changes in the stepsize, the overall scaling factor is limited to the range
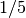 to 5.
to 5.
-
gsl_odeiv2_control *gsl_odeiv2_control_y_new(double eps_abs, double eps_rel)¶
This function creates a new control object which will keep the local error on each step within an absolute error of
eps_absand relative error ofeps_relwith respect to the solution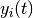 .
This is equivalent to the standard control object with
.
This is equivalent to the standard control object with a_y= 1 anda_dydt= 0.
-
gsl_odeiv2_control *gsl_odeiv2_control_yp_new(double eps_abs, double eps_rel)¶
This function creates a new control object which will keep the local error on each step within an absolute error of
eps_absand relative error ofeps_relwith respect to the derivatives of the solution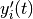 . This is equivalent to the standard control
object with
. This is equivalent to the standard control
object with a_y= 0 anda_dydt= 1.
-
gsl_odeiv2_control *gsl_odeiv2_control_scaled_new(double eps_abs, double eps_rel, double a_y, double a_dydt, const double scale_abs[], size_t dim)¶
This function creates a new control object which uses the same algorithm as
gsl_odeiv2_control_standard_new()but with an absolute error which is scaled for each component by the arrayscale_abs. The formula for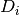 for this control object is,
for this control object is,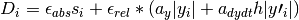
where
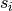 is the
is the 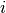 -th component of the array
-th component of the array scale_abs. The same error control heuristic is used by the Matlab ODE suite.
-
gsl_odeiv2_control *gsl_odeiv2_control_alloc(const gsl_odeiv2_control_type *T)¶
This function returns a pointer to a newly allocated instance of a control function of type
T. This function is only needed for defining new types of control functions. For most purposes the standard control functions described above should be sufficient.
-
int gsl_odeiv2_control_init(gsl_odeiv2_control *c, double eps_abs, double eps_rel, double a_y, double a_dydt)¶
This function initializes the control function
cwith the parameterseps_abs(absolute error),eps_rel(relative error),a_y(scaling factor for y) anda_dydt(scaling factor for derivatives).
-
void gsl_odeiv2_control_free(gsl_odeiv2_control *c)¶
This function frees all the memory associated with the control function
c.
-
int gsl_odeiv2_control_hadjust(gsl_odeiv2_control *c, gsl_odeiv2_step *s, const double y[], const double yerr[], const double dydt[], double *h)¶
This function adjusts the step-size
husing the control functionc, and the current values ofy,yerranddydt. The stepping functionstepis also needed to determine the order of the method. If the error in the y-valuesyerris found to be too large then the step-sizehis reduced and the function returnsGSL_ODEIV_HADJ_DEC. If the error is sufficiently small thenhmay be increased andGSL_ODEIV_HADJ_INCis returned. The function returnsGSL_ODEIV_HADJ_NILif the step-size is unchanged. The goal of the function is to estimate the largest step-size which satisfies the user-specified accuracy requirements for the current point.
-
const char *gsl_odeiv2_control_name(const gsl_odeiv2_control *c)¶
This function returns a pointer to the name of the control function. For example:
printf ("control method is '%s'\n", gsl_odeiv2_control_name (c));
would print something like
control method is 'standard'
-
int gsl_odeiv2_control_errlevel(gsl_odeiv2_control *c, const double y, const double dydt, const double h, const size_t ind, double *errlev)¶
This function calculates the desired error level of the
ind-th component toerrlev. It requires the value (y) and value of the derivative (dydt) of the component, and the current step sizeh.
-
int gsl_odeiv2_control_set_driver(gsl_odeiv2_control *c, const gsl_odeiv2_driver *d)¶
This function sets a pointer of the driver object
dfor control objectc.
Evolution¶
The evolution function combines the results of a stepping function and control function to reliably advance the solution forward one step using an acceptable step-size.
-
type gsl_odeiv2_evolve¶
This workspace contains parameters for controlling the evolution function
-
gsl_odeiv2_evolve *gsl_odeiv2_evolve_alloc(size_t dim)¶
This function returns a pointer to a newly allocated instance of an evolution function for a system of
dimdimensions.
-
int gsl_odeiv2_evolve_apply(gsl_odeiv2_evolve *e, gsl_odeiv2_control *con, gsl_odeiv2_step *step, const gsl_odeiv2_system *sys, double *t, double t1, double *h, double y[])¶
This function advances the system (
e,sys) from timetand positionyusing the stepping functionstep. The new time and position are stored intandyon output.The initial step-size is taken as
h. The control functionconis applied to check whether the local error estimated by the stepping functionstepusing step-sizehexceeds the required error tolerance. If the error is too high, the step is retried by callingstepwith a decreased step-size. This process is continued until an acceptable step-size is found. An estimate of the local error for the step can be obtained from the components of the arraye->yerr[].If the user-supplied functions defined in the system
sysreturnsGSL_EBADFUNC, the function returns immediately with the same return code. In this case the user must callgsl_odeiv2_step_reset()andgsl_odeiv2_evolve_reset()before calling this function again.Otherwise, if the user-supplied functions defined in the system
sysor the stepping functionstepreturn a status other thanGSL_SUCCESS, the step is retried with a decreased step-size. If the step-size decreases below machine precision, a status ofGSL_FAILUREis returned if the user functions returnedGSL_SUCCESS. Otherwise the value returned by user function is returned. If no acceptable step can be made,tandywill be restored to their pre-step values andhcontains the final attempted step-size.If the step is successful the function returns a suggested step-size for the next step in
h. The maximum timet1is guaranteed not to be exceeded by the time-step. On the final time-step the value oftwill be set tot1exactly.
-
int gsl_odeiv2_evolve_apply_fixed_step(gsl_odeiv2_evolve *e, gsl_odeiv2_control *con, gsl_odeiv2_step *step, const gsl_odeiv2_system *sys, double *t, const double h, double y[])¶
This function advances the ODE-system (
e,sys,con) from timetand positionyusing the stepping functionstepby a specified step sizeh. If the local error estimated by the stepping function exceeds the desired error level, the step is not taken and the function returnsGSL_FAILURE. Otherwise the value returned by user function is returned.
-
int gsl_odeiv2_evolve_reset(gsl_odeiv2_evolve *e)¶
This function resets the evolution function
e. It should be used whenever the next use ofewill not be a continuation of a previous step.
-
void gsl_odeiv2_evolve_free(gsl_odeiv2_evolve *e)¶
This function frees all the memory associated with the evolution function
e.
-
int gsl_odeiv2_evolve_set_driver(gsl_odeiv2_evolve *e, const gsl_odeiv2_driver *d)¶
This function sets a pointer of the driver object
dfor evolve objecte.
If a system has discontinuous changes in the derivatives at known
points, it is advisable to evolve the system between each discontinuity
in sequence. For example, if a step-change in an external driving
force occurs at times 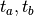 and
and 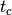 then evolution
should be carried out over the ranges
then evolution
should be carried out over the ranges 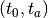 ,
,
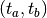 ,
, 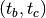 , and
, and 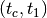 separately
and not directly over the range
separately
and not directly over the range 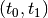 .
.
Driver¶
The driver object is a high level wrapper that combines the evolution, control and stepper objects for easy use.
-
gsl_odeiv2_driver *gsl_odeiv2_driver_alloc_y_new(const gsl_odeiv2_system *sys, const gsl_odeiv2_step_type *T, const double hstart, const double epsabs, const double epsrel)¶
-
gsl_odeiv2_driver *gsl_odeiv2_driver_alloc_yp_new(const gsl_odeiv2_system *sys, const gsl_odeiv2_step_type *T, const double hstart, const double epsabs, const double epsrel)¶
-
gsl_odeiv2_driver *gsl_odeiv2_driver_alloc_standard_new(const gsl_odeiv2_system *sys, const gsl_odeiv2_step_type *T, const double hstart, const double epsabs, const double epsrel, const double a_y, const double a_dydt)¶
-
gsl_odeiv2_driver *gsl_odeiv2_driver_alloc_scaled_new(const gsl_odeiv2_system *sys, const gsl_odeiv2_step_type *T, const double hstart, const double epsabs, const double epsrel, const double a_y, const double a_dydt, const double scale_abs[])¶
These functions return a pointer to a newly allocated instance of a driver object. The functions automatically allocate and initialise the evolve, control and stepper objects for ODE system
sysusing stepper typeT. The initial step size is given inhstart. The rest of the arguments follow the syntax and semantics of the control functions with same name (gsl_odeiv2_control_*_new).
-
int gsl_odeiv2_driver_set_hmin(gsl_odeiv2_driver *d, const double hmin)¶
The function sets a minimum for allowed step size
hminfor driverd. Default value is 0.
-
int gsl_odeiv2_driver_set_hmax(gsl_odeiv2_driver *d, const double hmax)¶
The function sets a maximum for allowed step size
hmaxfor driverd. Default value isGSL_DBL_MAX.
-
int gsl_odeiv2_driver_set_nmax(gsl_odeiv2_driver *d, const unsigned long int nmax)¶
The function sets a maximum for allowed number of steps
nmaxfor driverd. Default value of 0 sets no limit for steps.
-
int gsl_odeiv2_driver_apply(gsl_odeiv2_driver *d, double *t, const double t1, double y[])¶
This function evolves the driver system
dfromttot1. Initially vectoryshould contain the values of dependent variables at pointt. If the function is unable to complete the calculation, an error code fromgsl_odeiv2_evolve_apply()is returned, andtandycontain the values from last successful step.If maximum number of steps is reached, a value of
GSL_EMAXITERis returned. If the step size drops below minimum value, the function returns withGSL_ENOPROG. If the user-supplied functions defined in the systemsysreturnsGSL_EBADFUNC, the function returns immediately with the same return code. In this case the user must callgsl_odeiv2_driver_reset()before calling this function again.
-
int gsl_odeiv2_driver_apply_fixed_step(gsl_odeiv2_driver *d, double *t, const double h, const unsigned long int n, double y[])¶
This function evolves the driver system
dfromtwithnsteps of sizeh. If the function is unable to complete the calculation, an error code fromgsl_odeiv2_evolve_apply_fixed_step()is returned, andtandycontain the values from last successful step.
-
int gsl_odeiv2_driver_reset(gsl_odeiv2_driver *d)¶
This function resets the evolution and stepper objects.
-
int gsl_odeiv2_driver_reset_hstart(gsl_odeiv2_driver *d, const double hstart)¶
The routine resets the evolution and stepper objects and sets new initial step size to
hstart. This function can be used e.g. to change the direction of integration.
-
int gsl_odeiv2_driver_free(gsl_odeiv2_driver *d)¶
This function frees the driver object, and the related evolution, stepper and control objects.
Examples¶
The following program solves the second-order nonlinear Van der Pol oscillator equation,
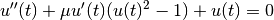
This can be converted into a first order system suitable for use with
the routines described in this chapter by introducing a separate
variable for the velocity, 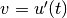 ,
,
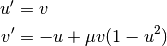
The program begins by defining functions for these derivatives and
their Jacobian. The main function uses driver level functions to solve
the problem. The program evolves the solution from 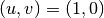 at
at 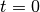 to
to 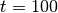 . The step-size
. The step-size 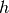 is
automatically adjusted by the controller to maintain an absolute
accuracy of
is
automatically adjusted by the controller to maintain an absolute
accuracy of 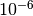 in the function values
in the function values 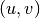 .
The loop in the example prints the solution at the points
.
The loop in the example prints the solution at the points
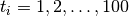 .
.
#include <stdio.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_odeiv2.h>
int
func (double t, const double y[], double f[],
void *params)
{
(void)(t); /* avoid unused parameter warning */
double mu = *(double *)params;
f[0] = y[1];
f[1] = -y[0] - mu*y[1]*(y[0]*y[0] - 1);
return GSL_SUCCESS;
}
int
jac (double t, const double y[], double *dfdy,
double dfdt[], void *params)
{
(void)(t); /* avoid unused parameter warning */
double mu = *(double *)params;
gsl_matrix_view dfdy_mat
= gsl_matrix_view_array (dfdy, 2, 2);
gsl_matrix * m = &dfdy_mat.matrix;
gsl_matrix_set (m, 0, 0, 0.0);
gsl_matrix_set (m, 0, 1, 1.0);
gsl_matrix_set (m, 1, 0, -2.0*mu*y[0]*y[1] - 1.0);
gsl_matrix_set (m, 1, 1, -mu*(y[0]*y[0] - 1.0));
dfdt[0] = 0.0;
dfdt[1] = 0.0;
return GSL_SUCCESS;
}
int
main (void)
{
double mu = 10;
gsl_odeiv2_system sys = {func, jac, 2, &mu};
gsl_odeiv2_driver * d =
gsl_odeiv2_driver_alloc_y_new (&sys, gsl_odeiv2_step_rk8pd,
1e-6, 1e-6, 0.0);
int i;
double t = 0.0, t1 = 100.0;
double y[2] = { 1.0, 0.0 };
for (i = 1; i <= 100; i++)
{
double ti = i * t1 / 100.0;
int status = gsl_odeiv2_driver_apply (d, &t, ti, y);
if (status != GSL_SUCCESS)
{
printf ("error, return value=%d\n", status);
break;
}
printf ("%.5e %.5e %.5e\n", t, y[0], y[1]);
}
gsl_odeiv2_driver_free (d);
return 0;
}
The user can work with the lower level functions directly, as in the following example. In this case an intermediate result is printed after each successful step instead of equidistant time points.
int
main (void)
{
const gsl_odeiv2_step_type * T
= gsl_odeiv2_step_rk8pd;
gsl_odeiv2_step * s
= gsl_odeiv2_step_alloc (T, 2);
gsl_odeiv2_control * c
= gsl_odeiv2_control_y_new (1e-6, 0.0);
gsl_odeiv2_evolve * e
= gsl_odeiv2_evolve_alloc (2);
double mu = 10;
gsl_odeiv2_system sys = {func, jac, 2, &mu};
double t = 0.0, t1 = 100.0;
double h = 1e-6;
double y[2] = { 1.0, 0.0 };
while (t < t1)
{
int status = gsl_odeiv2_evolve_apply (e, c, s,
&sys,
&t, t1,
&h, y);
if (status != GSL_SUCCESS)
break;
printf ("%.5e %.5e %.5e\n", t, y[0], y[1]);
}
gsl_odeiv2_evolve_free (e);
gsl_odeiv2_control_free (c);
gsl_odeiv2_step_free (s);
return 0;
}
For functions with multiple parameters, the appropriate information
can be passed in through the params argument in
gsl_odeiv2_system definition (mu in this example) by using
a pointer to a struct.
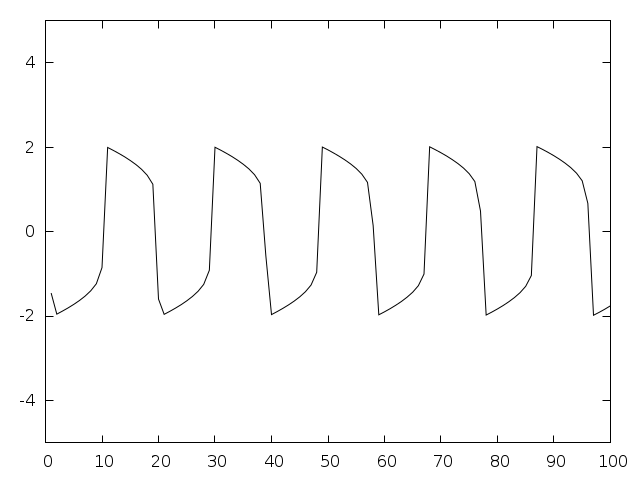
Fig. 21 Numerical solution of the Van der Pol oscillator equation using Prince-Dormand 8th order Runge-Kutta.¶
It is also possible to work with a non-adaptive integrator, using only
the stepping function itself,
gsl_odeiv2_driver_apply_fixed_step() or
gsl_odeiv2_evolve_apply_fixed_step(). The following program uses
the driver level function, with fourth-order
Runge-Kutta stepping function with a fixed stepsize of
0.001.
int
main (void)
{
double mu = 10;
gsl_odeiv2_system sys = { func, jac, 2, &mu };
gsl_odeiv2_driver *d =
gsl_odeiv2_driver_alloc_y_new (&sys, gsl_odeiv2_step_rk4,
1e-3, 1e-8, 1e-8);
double t = 0.0;
double y[2] = { 1.0, 0.0 };
int i, s;
for (i = 0; i < 100; i++)
{
s = gsl_odeiv2_driver_apply_fixed_step (d, &t, 1e-3, 1000, y);
if (s != GSL_SUCCESS)
{
printf ("error: driver returned %d\n", s);
break;
}
printf ("%.5e %.5e %.5e\n", t, y[0], y[1]);
}
gsl_odeiv2_driver_free (d);
return s;
}
References and Further Reading¶
Ascher, U.M., Petzold, L.R., Computer Methods for Ordinary Differential and Differential-Algebraic Equations, SIAM, Philadelphia, 1998.
Hairer, E., Norsett, S. P., Wanner, G., Solving Ordinary Differential Equations I: Nonstiff Problems, Springer, Berlin, 1993.
Hairer, E., Wanner, G., Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, Springer, Berlin, 1996.
Many of the basic Runge-Kutta formulas can be found in the Handbook of Mathematical Functions,
Abramowitz & Stegun (eds.), Handbook of Mathematical Functions, Section 25.5.
The implicit Bulirsch-Stoer algorithm bsimp is described in the
following paper,
G. Bader and P. Deuflhard, “A Semi-Implicit Mid-Point Rule for Stiff Systems of Ordinary Differential Equations.”, Numer.: Math.: 41, 373–398, 1983.
The Adams and BDF multistep methods msadams and msbdf
are based on the following articles,
G. D. Byrne and A. C. Hindmarsh, “A Polyalgorithm for the Numerical Solution of Ordinary Differential Equations.”, ACM Trans. Math. Software, 1, 71–96, 1975.
P. N. Brown, G. D. Byrne and A. C. Hindmarsh, “VODE: A Variable-coefficient ODE Solver.”, SIAM J. Sci. Stat. Comput. 10, 1038–1051, 1989.
A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker and C. S. Woodward, “SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers.”, ACM Trans. Math. Software 31, 363–396, 2005.