Interpolation¶
This chapter describes functions for performing interpolation. The library provides a variety of interpolation methods, including Cubic, Akima, and Steffen splines. The interpolation types are interchangeable, allowing different methods to be used without recompiling. Interpolations can be defined for both normal and periodic boundary conditions. Additional functions are available for computing derivatives and integrals of interpolating functions. Routines are provided for interpolating both one and two dimensional datasets.
These interpolation methods produce curves that pass through each datapoint. To interpolate noisy data with a smoothing curve see Basis Splines.
The functions described in this section are declared in the header files
gsl_interp.h and gsl_spline.h.
Introduction to 1D Interpolation¶
Given a set of data points 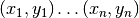 the
routines described in this section compute a continuous interpolating
function
the
routines described in this section compute a continuous interpolating
function 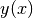 such that
such that 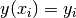 . The interpolation
is piecewise smooth, and its behavior at the end-points is determined by
the type of interpolation used.
. The interpolation
is piecewise smooth, and its behavior at the end-points is determined by
the type of interpolation used.
1D Interpolation Functions¶
The interpolation function for a given dataset is stored in a
gsl_interp object. These are created by the following functions.
-
type gsl_interp¶
Workspace for 1D interpolation
-
gsl_interp *gsl_interp_alloc(const gsl_interp_type *T, size_t size)¶
This function returns a pointer to a newly allocated interpolation object of type
Tforsizedata-points.
-
int gsl_interp_init(gsl_interp *interp, const double xa[], const double ya[], size_t size)¶
This function initializes the interpolation object
interpfor the data (xa,ya) wherexaandyaare arrays of sizesize. The interpolation object (gsl_interp) does not save the data arraysxaandyaand only stores the static state computed from the data. Thexadata array is always assumed to be strictly ordered, with increasing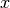 values;
the behavior for other arrangements is not defined.
values;
the behavior for other arrangements is not defined.
-
void gsl_interp_free(gsl_interp *interp)¶
This function frees the interpolation object
interp.
1D Interpolation Types¶
The interpolation library provides the following interpolation types:
-
type gsl_interp_type¶
-
gsl_interp_type *gsl_interp_linear¶
Linear interpolation. This interpolation method does not require any additional memory.
-
gsl_interp_type *gsl_interp_polynomial¶
Polynomial interpolation. This method should only be used for interpolating small numbers of points because polynomial interpolation introduces large oscillations, even for well-behaved datasets. The number of terms in the interpolating polynomial is equal to the number of points.
-
gsl_interp_type *gsl_interp_cspline¶
Cubic spline with natural boundary conditions. The resulting curve is piecewise cubic on each interval, with matching first and second derivatives at the supplied data-points. The second derivative is chosen to be zero at the first point and last point.
-
gsl_interp_type *gsl_interp_cspline_periodic¶
Cubic spline with periodic boundary conditions. The resulting curve is piecewise cubic on each interval, with matching first and second derivatives at the supplied data-points. The derivatives at the first and last points are also matched. Note that the last point in the data must have the same y-value as the first point, otherwise the resulting periodic interpolation will have a discontinuity at the boundary.
-
gsl_interp_type *gsl_interp_akima¶
Non-rounded Akima spline with natural boundary conditions. This method uses the non-rounded corner algorithm of Wodicka.
-
gsl_interp_type *gsl_interp_akima_periodic¶
Non-rounded Akima spline with periodic boundary conditions. This method uses the non-rounded corner algorithm of Wodicka.
-
gsl_interp_type *gsl_interp_steffen¶
Steffen’s method guarantees the monotonicity of the interpolating function between the given data points. Therefore, minima and maxima can only occur exactly at the data points, and there can never be spurious oscillations between data points. The interpolated function is piecewise cubic in each interval. The resulting curve and its first derivative are guaranteed to be continuous, but the second derivative may be discontinuous.
-
gsl_interp_type *gsl_interp_linear¶
The following related functions are available:
-
const char *gsl_interp_name(const gsl_interp *interp)¶
This function returns the name of the interpolation type used by
interp. For example:printf ("interp uses '%s' interpolation.\n", gsl_interp_name (interp));
would print something like:
interp uses 'cspline' interpolation.
-
unsigned int gsl_interp_min_size(const gsl_interp *interp)¶
-
unsigned int gsl_interp_type_min_size(const gsl_interp_type *T)¶
These functions return the minimum number of points required by the interpolation object
interpor interpolation typeT. For example, Akima spline interpolation requires a minimum of 5 points.
1D Index Look-up and Acceleration¶
The state of searches can be stored in a gsl_interp_accel object,
which is a kind of iterator for interpolation lookups.
-
type gsl_interp_accel¶
This workspace stores state variables for interpolation lookups. It caches the previous value of an index lookup. When the subsequent interpolation point falls in the same interval its index value can be returned immediately.
-
size_t gsl_interp_bsearch(const double x_array[], double x, size_t index_lo, size_t index_hi)¶
This function returns the index
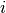 of the array
of the array x_arraysuch thatx_array[i] <= x < x_array[i+1]. The index is searched for in the range [index_lo,index_hi]. An inline version of this function is used whenHAVE_INLINEis defined.
-
gsl_interp_accel *gsl_interp_accel_alloc(void)¶
This function returns a pointer to an accelerator object, which is a kind of iterator for interpolation lookups. It tracks the state of lookups, thus allowing for application of various acceleration strategies. When multiple interpolants are in use, the same accelerator object may be used for all datasets with the same domain (
x_array), but different accelerators should be used for data defined on different domains.
-
size_t gsl_interp_accel_find(gsl_interp_accel *a, const double x_array[], size_t size, double x)¶
This function performs a lookup action on the data array
x_arrayof sizesize, using the given acceleratora. This is how lookups are performed during evaluation of an interpolation. The function returns an index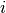 such that
such that x_array[i] <= x < x_array[i+1]. An inline version of this function is used whenHAVE_INLINEis defined.
-
int gsl_interp_accel_reset(gsl_interp_accel *acc);¶
This function reinitializes the accelerator object
acc. It should be used when the cached information is no longer applicable—for example, when switching to a new dataset.
-
void gsl_interp_accel_free(gsl_interp_accel *acc)¶
This function frees the accelerator object
acc.
1D Evaluation of Interpolating Functions¶
-
double gsl_interp_eval(const gsl_interp *interp, const double xa[], const double ya[], double x, gsl_interp_accel *acc)¶
-
int gsl_interp_eval_e(const gsl_interp *interp, const double xa[], const double ya[], double x, gsl_interp_accel *acc, double *y)¶
These functions return the interpolated value of
yfor a given pointx, using the interpolation objectinterp, data arraysxaandyaand the acceleratoracc. Whenxis outside the range ofxa, the error codeGSL_EDOMis returned with a value ofGSL_NANfory.
-
double gsl_interp_eval_deriv(const gsl_interp *interp, const double xa[], const double ya[], double x, gsl_interp_accel *acc)¶
-
int gsl_interp_eval_deriv_e(const gsl_interp *interp, const double xa[], const double ya[], double x, gsl_interp_accel *acc, double *d)¶
These functions return the derivative
dof an interpolated function for a given pointx, using the interpolation objectinterp, data arraysxaandyaand the acceleratoracc.
-
double gsl_interp_eval_deriv2(const gsl_interp *interp, const double xa[], const double ya[], double x, gsl_interp_accel *acc)¶
-
int gsl_interp_eval_deriv2_e(const gsl_interp *interp, const double xa[], const double ya[], double x, gsl_interp_accel *acc, double *d2)¶
These functions return the second derivative
d2of an interpolated function for a given pointx, using the interpolation objectinterp, data arraysxaandyaand the acceleratoracc.
-
double gsl_interp_eval_integ(const gsl_interp *interp, const double xa[], const double ya[], double a, double b, gsl_interp_accel *acc)¶
-
int gsl_interp_eval_integ_e(const gsl_interp *interp, const double xa[], const double ya[], double a, double b, gsl_interp_accel *acc, double *result)¶
These functions return the numerical integral
resultof an interpolated function over the range [a,b], using the interpolation objectinterp, data arraysxaandyaand the acceleratoracc.
1D Higher-level Interface¶
The functions described in the previous sections required the user to
supply pointers to the 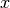 and
and 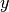 arrays on each call. The
following functions are equivalent to the corresponding
arrays on each call. The
following functions are equivalent to the corresponding
gsl_interp functions but maintain a copy of this data in the
gsl_spline object. This removes the need to pass both xa
and ya as arguments on each evaluation. These functions are
defined in the header file gsl_spline.h.
-
type gsl_spline¶
This workspace provides a higher level interface for the
gsl_interpobject
-
gsl_spline *gsl_spline_alloc(const gsl_interp_type *T, size_t size)¶
-
int gsl_spline_init(gsl_spline *spline, const double xa[], const double ya[], size_t size)¶
-
void gsl_spline_free(gsl_spline *spline)¶
-
const char *gsl_spline_name(const gsl_spline *spline)¶
-
unsigned int gsl_spline_min_size(const gsl_spline *spline)¶
-
double gsl_spline_eval(const gsl_spline *spline, double x, gsl_interp_accel *acc)¶
-
int gsl_spline_eval_e(const gsl_spline *spline, double x, gsl_interp_accel *acc, double *y)¶
-
double gsl_spline_eval_deriv(const gsl_spline *spline, double x, gsl_interp_accel *acc)¶
-
int gsl_spline_eval_deriv_e(const gsl_spline *spline, double x, gsl_interp_accel *acc, double *d)¶
-
double gsl_spline_eval_deriv2(const gsl_spline *spline, double x, gsl_interp_accel *acc)¶
-
int gsl_spline_eval_deriv2_e(const gsl_spline *spline, double x, gsl_interp_accel *acc, double *d2)¶
-
double gsl_spline_eval_integ(const gsl_spline *spline, double a, double b, gsl_interp_accel *acc)¶
-
int gsl_spline_eval_integ_e(const gsl_spline *spline, double a, double b, gsl_interp_accel *acc, double *result)¶
1D Interpolation Example Programs¶
The following program demonstrates the use of the interpolation and
spline functions. It computes a cubic spline interpolation of the
10-point dataset 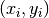 where
where 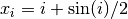 and
and
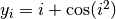 for
for 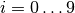 .
.
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_spline.h>
int
main (void)
{
int i;
double xi, yi, x[10], y[10];
printf ("#m=0,S=17\n");
for (i = 0; i < 10; i++)
{
x[i] = i + 0.5 * sin (i);
y[i] = i + cos (i * i);
printf ("%g %g\n", x[i], y[i]);
}
printf ("#m=1,S=0\n");
{
gsl_interp_accel *acc
= gsl_interp_accel_alloc ();
gsl_spline *spline
= gsl_spline_alloc (gsl_interp_cspline, 10);
gsl_spline_init (spline, x, y, 10);
for (xi = x[0]; xi < x[9]; xi += 0.01)
{
yi = gsl_spline_eval (spline, xi, acc);
printf ("%g %g\n", xi, yi);
}
gsl_spline_free (spline);
gsl_interp_accel_free (acc);
}
return 0;
}
The output is designed to be used with the GNU plotutils
graph program:
$ ./a.out > interp.dat
$ graph -T ps < interp.dat > interp.ps
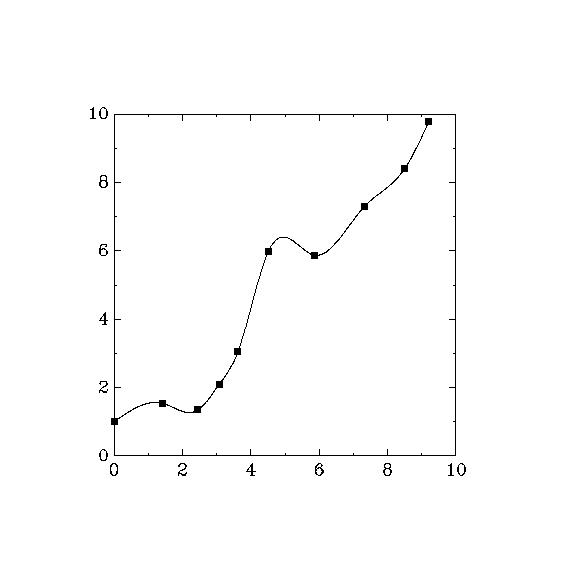
Fig. 22 Cubic spline interpolation¶
Fig. 22 shows a smooth interpolation of the original points. The
interpolation method can be changed simply by varying the first argument of
gsl_spline_alloc().
The next program demonstrates a periodic cubic spline with 4 data points. Note that the first and last points must be supplied with the same y-value for a periodic spline.
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_spline.h>
int
main (void)
{
int N = 4;
double x[4] = {0.00, 0.10, 0.27, 0.30};
double y[4] = {0.15, 0.70, -0.10, 0.15};
/* Note: y[0] == y[3] for periodic data */
gsl_interp_accel *acc = gsl_interp_accel_alloc ();
const gsl_interp_type *t = gsl_interp_cspline_periodic;
gsl_spline *spline = gsl_spline_alloc (t, N);
int i; double xi, yi;
printf ("#m=0,S=5\n");
for (i = 0; i < N; i++)
{
printf ("%g %g\n", x[i], y[i]);
}
printf ("#m=1,S=0\n");
gsl_spline_init (spline, x, y, N);
for (i = 0; i <= 100; i++)
{
xi = (1 - i / 100.0) * x[0] + (i / 100.0) * x[N-1];
yi = gsl_spline_eval (spline, xi, acc);
printf ("%g %g\n", xi, yi);
}
gsl_spline_free (spline);
gsl_interp_accel_free (acc);
return 0;
}
The output can be plotted with GNU graph:
$ ./a.out > interp.dat
$ graph -T ps < interp.dat > interp.ps
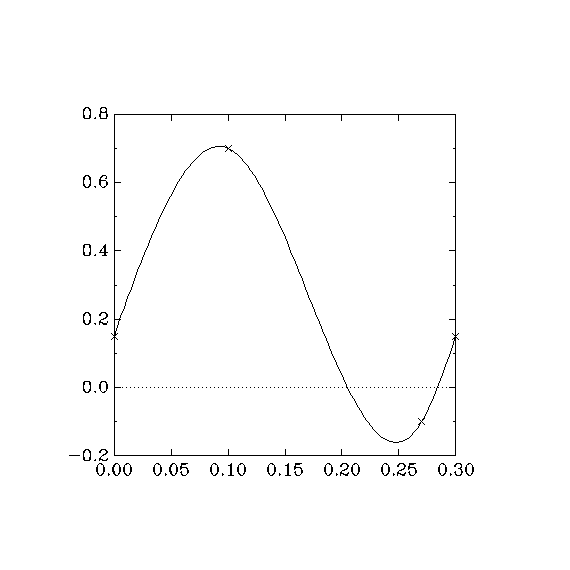
Fig. 23 Periodic cubic spline interpolation¶
Fig. 23 shows a periodic interpolation of the original points. The slope of the fitted curve is the same at the beginning and end of the data, and the second derivative is also.
The next program illustrates the difference between the cubic spline, Akima, and Steffen interpolation types on a difficult dataset.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_spline.h>
int
main(void)
{
size_t i;
const size_t N = 9;
/* this dataset is taken from
* J. M. Hyman, Accurate Monotonicity preserving cubic interpolation,
* SIAM J. Sci. Stat. Comput. 4, 4, 1983. */
const double x[] = { 7.99, 8.09, 8.19, 8.7, 9.2,
10.0, 12.0, 15.0, 20.0 };
const double y[] = { 0.0, 2.76429e-5, 4.37498e-2,
0.169183, 0.469428, 0.943740,
0.998636, 0.999919, 0.999994 };
gsl_interp_accel *acc = gsl_interp_accel_alloc();
gsl_spline *spline_cubic = gsl_spline_alloc(gsl_interp_cspline, N);
gsl_spline *spline_akima = gsl_spline_alloc(gsl_interp_akima, N);
gsl_spline *spline_steffen = gsl_spline_alloc(gsl_interp_steffen, N);
gsl_spline_init(spline_cubic, x, y, N);
gsl_spline_init(spline_akima, x, y, N);
gsl_spline_init(spline_steffen, x, y, N);
for (i = 0; i < N; ++i)
printf("%g %g\n", x[i], y[i]);
printf("\n\n");
for (i = 0; i <= 100; ++i)
{
double xi = (1 - i / 100.0) * x[0] + (i / 100.0) * x[N-1];
double yi_cubic = gsl_spline_eval(spline_cubic, xi, acc);
double yi_akima = gsl_spline_eval(spline_akima, xi, acc);
double yi_steffen = gsl_spline_eval(spline_steffen, xi, acc);
printf("%g %g %g %g\n", xi, yi_cubic, yi_akima, yi_steffen);
}
gsl_spline_free(spline_cubic);
gsl_spline_free(spline_akima);
gsl_spline_free(spline_steffen);
gsl_interp_accel_free(acc);
return 0;
}
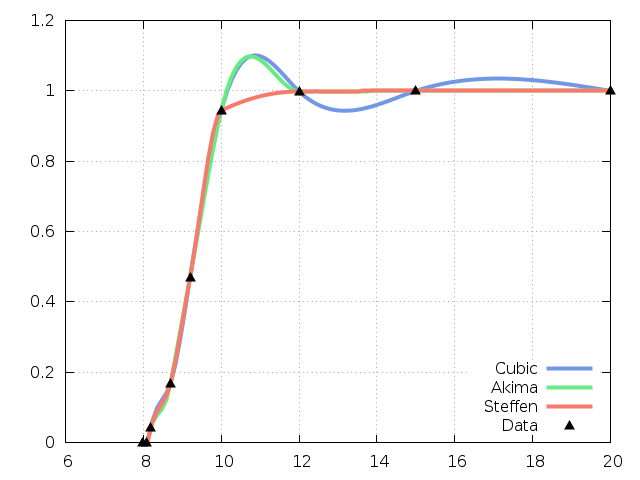
Fig. 24 Comparison of different 1D interpolation methods¶
The output is shown in Fig. 24. The cubic method exhibits a local maxima between the 6th and 7th data points and continues oscillating for the rest of the data. Akima also shows a local maxima but recovers and follows the data well after the 7th grid point. Steffen preserves monotonicity in all intervals and does not exhibit oscillations, at the expense of having a discontinuous second derivative.
Introduction to 2D Interpolation¶
Given a set of 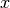 coordinates
coordinates 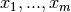 and a set of
and a set of
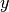 coordinates
coordinates 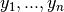 , each in increasing order,
plus a set of function values
, each in increasing order,
plus a set of function values 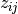 for each grid point
for each grid point 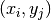 , the routines described in this
section compute a continuous interpolation function
, the routines described in this
section compute a continuous interpolation function 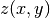 such
that
such
that 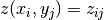 .
.
2D Interpolation Functions¶
The interpolation function for a given dataset is stored in a
gsl_interp2d object. These are created by the following functions.
-
type gsl_interp2d¶
Workspace for 2D interpolation
-
gsl_interp2d *gsl_interp2d_alloc(const gsl_interp2d_type *T, const size_t xsize, const size_t ysize)¶
This function returns a pointer to a newly allocated interpolation object of type
Tforxsizegrid points in the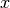 direction and
direction and ysizegrid points in the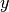 direction.
direction.
-
int gsl_interp2d_init(gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const size_t xsize, const size_t ysize)¶
This function initializes the interpolation object
interpfor the data (xa,ya,za) wherexaandyaare arrays of the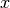 and
and 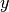 grid points of size
grid points of size xsizeandysizerespectively, andzais an array of function values of sizexsize*ysize. The interpolation object (gsl_interp2d) does not save the data arraysxa,ya, andzaand only stores the static state computed from the data. Thexaandyadata arrays are always assumed to be strictly ordered, with increasing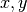 values;
the behavior for other arrangements is not defined.
values;
the behavior for other arrangements is not defined.
-
void gsl_interp2d_free(gsl_interp2d *interp)¶
This function frees the interpolation object
interp.
2D Interpolation Grids¶
The 2D interpolation routines access the function values 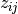 with the following ordering:
with the following ordering:
![z_{ij} = za[j*xsize + i]](_images/math/1974b840b0c6c8259f4db51fbe10c5bd69efd3c3.png)
with 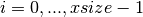 and
and 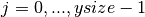 . However,
for ease of use, the following functions are provided to add and retrieve
elements from the function grid without requiring knowledge of the
internal ordering.
. However,
for ease of use, the following functions are provided to add and retrieve
elements from the function grid without requiring knowledge of the
internal ordering.
-
int gsl_interp2d_set(const gsl_interp2d *interp, double za[], const size_t i, const size_t j, const double z)¶
This function sets the value
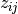 for grid point
(
for grid point
(i,j) of the arrayzatoz.
-
double gsl_interp2d_get(const gsl_interp2d *interp, const double za[], const size_t i, const size_t j)¶
This function returns the value
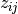 for grid point
(
for grid point
(i,j) stored in the arrayza.
-
size_t gsl_interp2d_idx(const gsl_interp2d *interp, const size_t i, const size_t j)¶
This function returns the index corresponding to the grid point (
i,j). The index is given by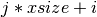 .
.
2D Interpolation Types¶
-
type gsl_interp2d_type¶
The interpolation library provides the following 2D interpolation types:
-
gsl_interp2d_type *gsl_interp2d_bilinear¶
Bilinear interpolation. This interpolation method does not require any additional memory.
-
gsl_interp2d_type *gsl_interp2d_bicubic¶
Bicubic interpolation.
-
gsl_interp2d_type *gsl_interp2d_bilinear¶
-
const char *gsl_interp2d_name(const gsl_interp2d *interp)¶
This function returns the name of the interpolation type used by
interp. For example:printf ("interp uses '%s' interpolation.\n", gsl_interp2d_name (interp));
would print something like:
interp uses 'bilinear' interpolation.
-
unsigned int gsl_interp2d_min_size(const gsl_interp2d *interp)¶
-
unsigned int gsl_interp2d_type_min_size(const gsl_interp2d_type *T)¶
These functions return the minimum number of points required by the interpolation object
interpor interpolation typeT. For example, bicubic interpolation requires a minimum of 4 points.
2D Evaluation of Interpolating Functions¶
-
double gsl_interp2d_eval(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_interp2d_eval_e(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *z)¶
These functions return the interpolated value of
zfor a given point (x,y), using the interpolation objectinterp, data arraysxa,ya, andzaand the acceleratorsxaccandyacc. Whenxis outside the range ofxaoryis outside the range ofya, the error codeGSL_EDOMis returned.
-
double gsl_interp2d_eval_extrap(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_interp2d_eval_extrap_e(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *z)¶
These functions return the interpolated value of
zfor a given point (x,y), using the interpolation objectinterp, data arraysxa,ya, andzaand the acceleratorsxaccandyacc. The functions perform no bounds checking, so whenxis outside the range ofxaoryis outside the range ofya, extrapolation is performed.
-
double gsl_interp2d_eval_deriv_x(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_interp2d_eval_deriv_x_e(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
These functions return the interpolated value
d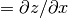 for a given point (
for a given point (x,y), using the interpolation objectinterp, data arraysxa,ya, andzaand the acceleratorsxaccandyacc. Whenxis outside the range ofxaoryis outside the range ofya, the error codeGSL_EDOMis returned.
-
double gsl_interp2d_eval_deriv_y(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_interp2d_eval_deriv_y_e(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
These functions return the interpolated value
d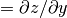 for a given point (
for a given point (x,y), using the interpolation objectinterp, data arraysxa,ya, andzaand the acceleratorsxaccandyacc. Whenxis outside the range ofxaoryis outside the range ofya, the error codeGSL_EDOMis returned.
-
double gsl_interp2d_eval_deriv_xx(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_interp2d_eval_deriv_xx_e(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
These functions return the interpolated value
d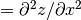 for a given point (
for a given point (x,y), using the interpolation objectinterp, data arraysxa,ya, andzaand the acceleratorsxaccandyacc. Whenxis outside the range ofxaoryis outside the range ofya, the error codeGSL_EDOMis returned.
-
double gsl_interp2d_eval_deriv_yy(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_interp2d_eval_deriv_yy_e(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
These functions return the interpolated value
d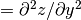 for a given point (
for a given point (x,y), using the interpolation objectinterp, data arraysxa,ya, andzaand the acceleratorsxaccandyacc. Whenxis outside the range ofxaoryis outside the range ofya, the error codeGSL_EDOMis returned.
-
double gsl_interp2d_eval_deriv_xy(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_interp2d_eval_deriv_xy_e(const gsl_interp2d *interp, const double xa[], const double ya[], const double za[], const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
These functions return the interpolated value
d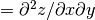 for a given point (
for a given point (x,y), using the interpolation objectinterp, data arraysxa,ya, andzaand the acceleratorsxaccandyacc. Whenxis outside the range ofxaoryis outside the range ofya, the error codeGSL_EDOMis returned.
2D Higher-level Interface¶
The functions described in the previous sections required the user to
supply pointers to the 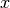 ,
, 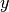 , and
, and  arrays on each call.
The following functions are equivalent to the corresponding
arrays on each call.
The following functions are equivalent to the corresponding
gsl_interp2d functions but maintain a copy of this data in the
gsl_spline2d object. This removes the need to pass xa,
ya, and za as arguments on each evaluation. These functions are
defined in the header file gsl_spline2d.h.
-
type gsl_spline2d¶
This workspace provides a higher level interface for the
gsl_interp2dobject
-
gsl_spline2d *gsl_spline2d_alloc(const gsl_interp2d_type *T, size_t xsize, size_t ysize)¶
-
int gsl_spline2d_init(gsl_spline2d *spline, const double xa[], const double ya[], const double za[], size_t xsize, size_t ysize)¶
-
void gsl_spline2d_free(gsl_spline2d *spline)¶
-
const char *gsl_spline2d_name(const gsl_spline2d *spline)¶
-
unsigned int gsl_spline2d_min_size(const gsl_spline2d *spline)¶
-
double gsl_spline2d_eval(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_spline2d_eval_e(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *z)¶
-
double gsl_spline2d_eval_extrap(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_spline2d_eval_extrap_e(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *z)¶
-
double gsl_spline2d_eval_deriv_x(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_spline2d_eval_deriv_x_e(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
-
double gsl_spline2d_eval_deriv_y(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_spline2d_eval_deriv_y_e(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
-
double gsl_spline2d_eval_deriv_xx(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_spline2d_eval_deriv_xx_e(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
-
double gsl_spline2d_eval_deriv_yy(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_spline2d_eval_deriv_yy_e(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
-
double gsl_spline2d_eval_deriv_xy(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc)¶
-
int gsl_spline2d_eval_deriv_xy_e(const gsl_spline2d *spline, const double x, const double y, gsl_interp_accel *xacc, gsl_interp_accel *yacc, double *d)¶
-
int gsl_spline2d_set(const gsl_spline2d *spline, double za[], const size_t i, const size_t j, const double z)¶
-
double gsl_spline2d_get(const gsl_spline2d *spline, const double za[], const size_t i, const size_t j)¶
This function returns the value
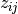 for grid point
(
for grid point
(i,j) stored in the arrayza.
2D Interpolation Example programs¶
The following example performs bilinear interpolation on the unit
square, using  values of
values of 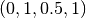 going clockwise
around the square.
going clockwise
around the square.
#include <stdio.h>
#include <stdlib.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_interp2d.h>
#include <gsl/gsl_spline2d.h>
int
main()
{
const gsl_interp2d_type *T = gsl_interp2d_bilinear;
const size_t N = 100; /* number of points to interpolate */
const double xa[] = { 0.0, 1.0 }; /* define unit square */
const double ya[] = { 0.0, 1.0 };
const size_t nx = sizeof(xa) / sizeof(double); /* x grid points */
const size_t ny = sizeof(ya) / sizeof(double); /* y grid points */
double *za = malloc(nx * ny * sizeof(double));
gsl_spline2d *spline = gsl_spline2d_alloc(T, nx, ny);
gsl_interp_accel *xacc = gsl_interp_accel_alloc();
gsl_interp_accel *yacc = gsl_interp_accel_alloc();
size_t i, j;
/* set z grid values */
gsl_spline2d_set(spline, za, 0, 0, 0.0);
gsl_spline2d_set(spline, za, 0, 1, 1.0);
gsl_spline2d_set(spline, za, 1, 1, 0.5);
gsl_spline2d_set(spline, za, 1, 0, 1.0);
/* initialize interpolation */
gsl_spline2d_init(spline, xa, ya, za, nx, ny);
/* interpolate N values in x and y and print out grid for plotting */
for (i = 0; i < N; ++i)
{
double xi = i / (N - 1.0);
for (j = 0; j < N; ++j)
{
double yj = j / (N - 1.0);
double zij = gsl_spline2d_eval(spline, xi, yj, xacc, yacc);
printf("%f %f %f\n", xi, yj, zij);
}
printf("\n");
}
gsl_spline2d_free(spline);
gsl_interp_accel_free(xacc);
gsl_interp_accel_free(yacc);
free(za);
return 0;
}
The results of the interpolation are shown in Fig. 25,
where the corners are labeled with their fixed  values.
values.
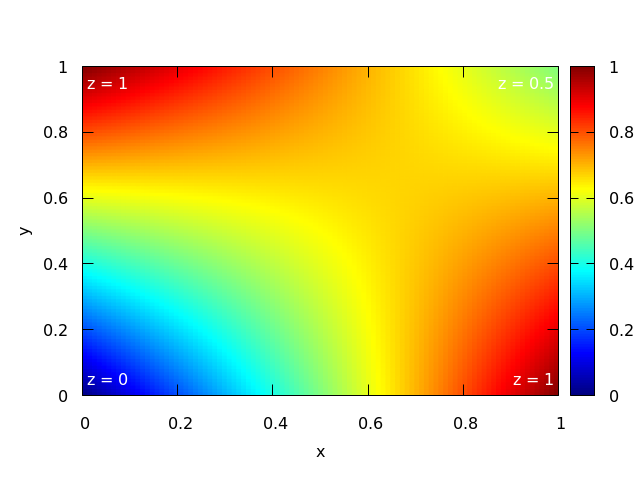
Fig. 25 2D interpolation example¶
References and Further Reading¶
Descriptions of the interpolation algorithms and further references can be found in the following publications:
C.W. Ueberhuber, Numerical Computation (Volume 1), Chapter 9 “Interpolation”, Springer (1997), ISBN 3-540-62058-3.
D.M. Young, R.T. Gregory, A Survey of Numerical Mathematics (Volume 1), Chapter 6.8, Dover (1988), ISBN 0-486-65691-8.
M. Steffen, A simple method for monotonic interpolation in one dimension, Astron. Astrophys. 239, 443-450, 1990.