One Dimensional Minimization¶
This chapter describes routines for finding minima of arbitrary one-dimensional functions. The library provides low level components for a variety of iterative minimizers and convergence tests. These can be combined by the user to achieve the desired solution, with full access to the intermediate steps of the algorithms. Each class of methods uses the same framework, so that you can switch between minimizers at runtime without needing to recompile your program. Each instance of a minimizer keeps track of its own state, allowing the minimizers to be used in multi-threaded programs.
The header file gsl_min.h contains prototypes for the
minimization functions and related declarations. To use the minimization
algorithms to find the maximum of a function simply invert its sign.
Overview¶
The minimization algorithms begin with a bounded region known to contain
a minimum. The region is described by a lower bound  and an
upper bound
and an
upper bound 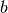 , with an estimate of the location of the minimum
, with an estimate of the location of the minimum
 , as shown in Fig. 28.
, as shown in Fig. 28.
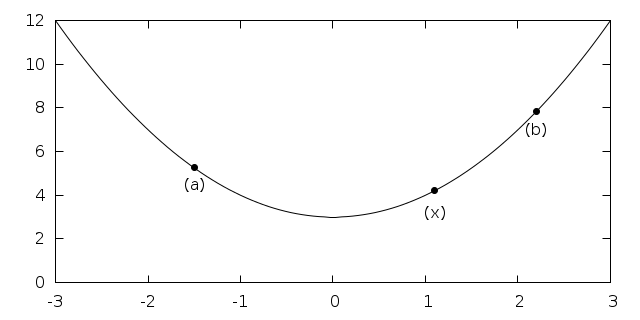
Fig. 28 Function with lower and upper bounds with an estimate of the minimum.¶
The value of the function at  must be less than the value of the
function at the ends of the interval,
must be less than the value of the
function at the ends of the interval,
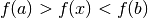
This condition guarantees that a minimum is contained somewhere within
the interval. On each iteration a new point 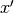 is selected using
one of the available algorithms. If the new point is a better estimate
of the minimum, i.e.: where
is selected using
one of the available algorithms. If the new point is a better estimate
of the minimum, i.e.: where 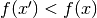 , then the current
estimate of the minimum
, then the current
estimate of the minimum  is updated. The new point also allows
the size of the bounded interval to be reduced, by choosing the most
compact set of points which satisfies the constraint
is updated. The new point also allows
the size of the bounded interval to be reduced, by choosing the most
compact set of points which satisfies the constraint 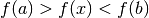 .
The interval is reduced until it encloses the true minimum to a
desired tolerance. This provides a best estimate of the location of the
minimum and a rigorous error estimate.
.
The interval is reduced until it encloses the true minimum to a
desired tolerance. This provides a best estimate of the location of the
minimum and a rigorous error estimate.
Several bracketing algorithms are available within a single framework. The user provides a high-level driver for the algorithm, and the library provides the individual functions necessary for each of the steps. There are three main phases of the iteration. The steps are,
initialize minimizer state,
s, for algorithmTupdate
susing the iterationTtest
sfor convergence, and repeat iteration if necessary
The state for the minimizers is held in a gsl_min_fminimizer
struct. The updating procedure uses only function evaluations (not
derivatives).
Caveats¶
Note that minimization functions can only search for one minimum at a time. When there are several minima in the search area, the first minimum to be found will be returned; however it is difficult to predict which of the minima this will be. In most cases, no error will be reported if you try to find a minimum in an area where there is more than one.
With all minimization algorithms it can be difficult to determine the
location of the minimum to full numerical precision. The behavior of the
function in the region of the minimum 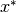 can be approximated by
a Taylor expansion,
can be approximated by
a Taylor expansion,
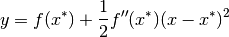
and the second term of this expansion can be lost when added to the
first term at finite precision. This magnifies the error in locating
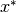 , making it proportional to
, making it proportional to 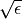 (where
(where
 is the relative accuracy of the floating point numbers).
For functions with higher order minima, such as
is the relative accuracy of the floating point numbers).
For functions with higher order minima, such as 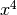 , the
magnification of the error is correspondingly worse. The best that can
be achieved is to converge to the limit of numerical accuracy in the
function values, rather than the location of the minimum itself.
, the
magnification of the error is correspondingly worse. The best that can
be achieved is to converge to the limit of numerical accuracy in the
function values, rather than the location of the minimum itself.
Initializing the Minimizer¶
-
type gsl_min_fminimizer¶
This is a workspace for minimizing functions.
-
gsl_min_fminimizer *gsl_min_fminimizer_alloc(const gsl_min_fminimizer_type *T)¶
This function returns a pointer to a newly allocated instance of a minimizer of type
T. For example, the following code creates an instance of a golden section minimizer:const gsl_min_fminimizer_type * T = gsl_min_fminimizer_goldensection; gsl_min_fminimizer * s = gsl_min_fminimizer_alloc (T);
If there is insufficient memory to create the minimizer then the function returns a null pointer and the error handler is invoked with an error code of
GSL_ENOMEM.
-
int gsl_min_fminimizer_set(gsl_min_fminimizer *s, gsl_function *f, double x_minimum, double x_lower, double x_upper)¶
This function sets, or resets, an existing minimizer
sto use the functionfand the initial search interval [x_lower,x_upper], with a guess for the location of the minimumx_minimum.If the interval given does not contain a minimum, then the function returns an error code of
GSL_EINVAL.
-
int gsl_min_fminimizer_set_with_values(gsl_min_fminimizer *s, gsl_function *f, double x_minimum, double f_minimum, double x_lower, double f_lower, double x_upper, double f_upper)¶
This function is equivalent to
gsl_min_fminimizer_set()but uses the valuesf_minimum,f_lowerandf_upperinstead of computingf(x_minimum),f(x_lower)andf(x_upper).
-
void gsl_min_fminimizer_free(gsl_min_fminimizer *s)¶
This function frees all the memory associated with the minimizer
s.
-
const char *gsl_min_fminimizer_name(const gsl_min_fminimizer *s)¶
This function returns a pointer to the name of the minimizer. For example:
printf ("s is a '%s' minimizer\n", gsl_min_fminimizer_name (s));
would print something like
s is a 'brent' minimizer.
Providing the function to minimize¶
You must provide a continuous function of one variable for the
minimizers to operate on. In order to allow for general parameters the
functions are defined by a gsl_function data type
(Providing the function to solve).
Iteration¶
The following functions drive the iteration of each algorithm. Each function performs one iteration to update the state of any minimizer of the corresponding type. The same functions work for all minimizers so that different methods can be substituted at runtime without modifications to the code.
-
int gsl_min_fminimizer_iterate(gsl_min_fminimizer *s)¶
This function performs a single iteration of the minimizer
s. If the iteration encounters an unexpected problem then an error code will be returned,GSL_EBADFUNCthe iteration encountered a singular point where the function evaluated to
InforNaN.GSL_FAILUREthe algorithm could not improve the current best approximation or bounding interval.
The minimizer maintains a current best estimate of the position of the minimum at all times, and the current interval bounding the minimum. This information can be accessed with the following auxiliary functions,
-
double gsl_min_fminimizer_x_minimum(const gsl_min_fminimizer *s)¶
This function returns the current estimate of the position of the minimum for the minimizer
s.
-
double gsl_min_fminimizer_x_upper(const gsl_min_fminimizer *s)¶
-
double gsl_min_fminimizer_x_lower(const gsl_min_fminimizer *s)¶
These functions return the current upper and lower bound of the interval for the minimizer
s.
-
double gsl_min_fminimizer_f_minimum(const gsl_min_fminimizer *s)¶
-
double gsl_min_fminimizer_f_upper(const gsl_min_fminimizer *s)¶
-
double gsl_min_fminimizer_f_lower(const gsl_min_fminimizer *s)¶
These functions return the value of the function at the current estimate of the minimum and at the upper and lower bounds of the interval for the minimizer
s.
Stopping Parameters¶
A minimization procedure should stop when one of the following conditions is true:
A minimum has been found to within the user-specified precision.
A user-specified maximum number of iterations has been reached.
An error has occurred.
The handling of these conditions is under user control. The function below allows the user to test the precision of the current result.
-
int gsl_min_test_interval(double x_lower, double x_upper, double epsabs, double epsrel)¶
This function tests for the convergence of the interval [
x_lower,x_upper] with absolute errorepsabsand relative errorepsrel. The test returnsGSL_SUCCESSif the following condition is achieved,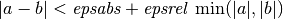
when the interval
![x = [a,b]](_images/math/b7dfd6c9d58c7a97d19cba79a64601e86331937f.png) does not include the origin. If the
interval includes the origin then
does not include the origin. If the
interval includes the origin then 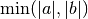 is replaced by
zero (which is the minimum value of
is replaced by
zero (which is the minimum value of  over the interval). This
ensures that the relative error is accurately estimated for minima close
to the origin.
over the interval). This
ensures that the relative error is accurately estimated for minima close
to the origin.This condition on the interval also implies that any estimate of the minimum
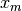 in the interval satisfies the same condition with respect
to the true minimum
in the interval satisfies the same condition with respect
to the true minimum 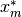 ,
,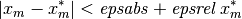
assuming that the true minimum
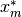 is contained within the interval.
is contained within the interval.
Minimization Algorithms¶
The minimization algorithms described in this section require an initial
interval which is guaranteed to contain a minimum—if  and
and
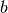 are the endpoints of the interval and
are the endpoints of the interval and  is an estimate
of the minimum then
is an estimate
of the minimum then 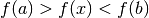 . This ensures that the
function has at least one minimum somewhere in the interval. If a valid
initial interval is used then these algorithm cannot fail, provided the
function is well-behaved.
. This ensures that the
function has at least one minimum somewhere in the interval. If a valid
initial interval is used then these algorithm cannot fail, provided the
function is well-behaved.
-
type gsl_min_fminimizer_type¶
-
gsl_min_fminimizer_type *gsl_min_fminimizer_goldensection¶
The golden section algorithm is the simplest method of bracketing the minimum of a function. It is the slowest algorithm provided by the library, with linear convergence.
On each iteration, the algorithm first compares the subintervals from the endpoints to the current minimum. The larger subinterval is divided in a golden section (using the famous ratio
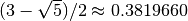 and the value of the function at this new point is
calculated. The new value is used with the constraint
and the value of the function at this new point is
calculated. The new value is used with the constraint 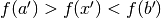 to a select new interval containing the minimum, by
discarding the least useful point. This procedure can be continued
indefinitely until the interval is sufficiently small. Choosing the
golden section as the bisection ratio can be shown to provide the
fastest convergence for this type of algorithm.
to a select new interval containing the minimum, by
discarding the least useful point. This procedure can be continued
indefinitely until the interval is sufficiently small. Choosing the
golden section as the bisection ratio can be shown to provide the
fastest convergence for this type of algorithm.
-
gsl_min_fminimizer_type *gsl_min_fminimizer_brent¶
The Brent minimization algorithm combines a parabolic interpolation with the golden section algorithm. This produces a fast algorithm which is still robust.
The outline of the algorithm can be summarized as follows: on each iteration Brent’s method approximates the function using an interpolating parabola through three existing points. The minimum of the parabola is taken as a guess for the minimum. If it lies within the bounds of the current interval then the interpolating point is accepted, and used to generate a smaller interval. If the interpolating point is not accepted then the algorithm falls back to an ordinary golden section step. The full details of Brent’s method include some additional checks to improve convergence.
-
gsl_min_fminimizer_type *gsl_min_fminimizer_quad_golden¶
This is a variant of Brent’s algorithm which uses the safeguarded step-length algorithm of Gill and Murray.
-
gsl_min_fminimizer_type *gsl_min_fminimizer_goldensection¶
Examples¶
The following program uses the Brent algorithm to find the minimum of
the function 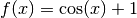 , which occurs at
, which occurs at 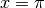 .
The starting interval is
.
The starting interval is 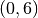 , with an initial guess for the
minimum of
, with an initial guess for the
minimum of 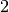 .
.
#include <stdio.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_min.h>
double fn1 (double x, void * params)
{
(void)(params); /* avoid unused parameter warning */
return cos(x) + 1.0;
}
int
main (void)
{
int status;
int iter = 0, max_iter = 100;
const gsl_min_fminimizer_type *T;
gsl_min_fminimizer *s;
double m = 2.0, m_expected = M_PI;
double a = 0.0, b = 6.0;
gsl_function F;
F.function = &fn1;
F.params = 0;
T = gsl_min_fminimizer_brent;
s = gsl_min_fminimizer_alloc (T);
gsl_min_fminimizer_set (s, &F, m, a, b);
printf ("using %s method\n",
gsl_min_fminimizer_name (s));
printf ("%5s [%9s, %9s] %9s %10s %9s\n",
"iter", "lower", "upper", "min",
"err", "err(est)");
printf ("%5d [%.7f, %.7f] %.7f %+.7f %.7f\n",
iter, a, b,
m, m - m_expected, b - a);
do
{
iter++;
status = gsl_min_fminimizer_iterate (s);
m = gsl_min_fminimizer_x_minimum (s);
a = gsl_min_fminimizer_x_lower (s);
b = gsl_min_fminimizer_x_upper (s);
status
= gsl_min_test_interval (a, b, 0.001, 0.0);
if (status == GSL_SUCCESS)
printf ("Converged:\n");
printf ("%5d [%.7f, %.7f] "
"%.7f %+.7f %.7f\n",
iter, a, b,
m, m - m_expected, b - a);
}
while (status == GSL_CONTINUE && iter < max_iter);
gsl_min_fminimizer_free (s);
return status;
}
Here are the results of the minimization procedure.
using brent method
iter [ lower, upper] min err err(est)
0 [0.0000000, 6.0000000] 2.0000000 -1.1415927 6.0000000
1 [2.0000000, 6.0000000] 3.5278640 +0.3862713 4.0000000
2 [2.0000000, 3.5278640] 3.1748217 +0.0332290 1.5278640
3 [2.0000000, 3.1748217] 3.1264576 -0.0151351 1.1748217
4 [3.1264576, 3.1748217] 3.1414743 -0.0001183 0.0483641
5 [3.1414743, 3.1748217] 3.1415930 +0.0000004 0.0333474
Converged:
6 [3.1414743, 3.1415930] 3.1415927 +0.0000000 0.0001187
References and Further Reading¶
Further information on Brent’s algorithm is available in the following book,
Richard Brent, Algorithms for minimization without derivatives, Prentice-Hall (1973), republished by Dover in paperback (2002), ISBN 0-486-41998-3.