Sparse BLAS Support¶

The Sparse Basic Linear Algebra Subprograms (BLAS) define a set of fundamental operations on vectors and sparse matrices which can be used to create optimized higher-level linear algebra functionality. GSL supports a limited number of BLAS operations for sparse matrices.

The header file gsl_spblas.h contains the prototypes for the sparse BLAS functions and related declarations.

Sparse BLAS operations¶

int gsl_spblas_dgemv(const CBLAS_TRANSPOSE_t TransA, const double alpha, const gsl_spmatrix *A, const gsl_vector *x, const double beta, gsl_vector *y)¶: This function computes the matrix-vector product and sum 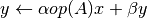$y \leftarrow \alpha op(A) x + \beta y$ , where 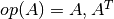$op(A) = A, A^T$ for TransA = CblasNoTrans, CblasTrans. In-place computations are not supported, so x and y must be distinct vectors. The matrix A may be in triplet or compressed format.

int gsl_spblas_dgemm(const double alpha, const gsl_spmatrix *A, const gsl_spmatrix *B, gsl_spmatrix *C)¶: This function computes the sparse matrix-matrix product 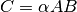$C = \alpha A B$ . The matrices must be in compressed format.

References and Further Reading¶

The algorithms used by these functions are described in the following sources:

Davis, T. A., Direct Methods for Sparse Linear Systems, SIAM, 2006.
CSparse software library, https://www.cise.ufl.edu/research/sparse/CSparse