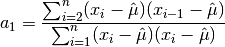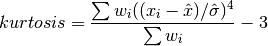Statistics¶
This chapter describes the statistical functions in the library. The basic statistical functions include routines to compute the mean, variance and standard deviation. More advanced functions allow you to calculate absolute deviations, skewness, and kurtosis as well as the median and arbitrary percentiles. The algorithms use recurrence relations to compute average quantities in a stable way, without large intermediate values that might overflow.
The functions are available in versions for datasets in the standard
floating-point and integer types. The versions for double precision
floating-point data have the prefix gsl_stats and are declared in
the header file gsl_statistics_double.h. The versions for integer
data have the prefix gsl_stats_int and are declared in the header
file gsl_statistics_int.h. All the functions operate on C
arrays with a stride parameter specifying the spacing between
elements.
Mean, Standard Deviation and Variance¶
-
double gsl_stats_mean(const double data[], size_t stride, size_t n)¶
This function returns the arithmetic mean of
data, a dataset of lengthnwith stridestride. The arithmetic mean, or sample mean, is denoted by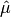 and defined as,
and defined as,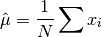
where
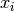 are the elements of the dataset
are the elements of the dataset data. For samples drawn from a gaussian distribution the variance of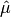 is
is 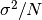 .
.
-
double gsl_stats_variance(const double data[], size_t stride, size_t n)¶
This function returns the estimated, or sample, variance of
data, a dataset of lengthnwith stridestride. The estimated variance is denoted by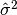 and is defined by,
and is defined by,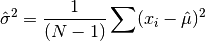
where
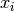 are the elements of the dataset
are the elements of the dataset data. Note that the normalization factor of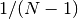 results from the derivation
of
results from the derivation
of 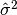 as an unbiased estimator of the population
variance
as an unbiased estimator of the population
variance 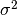 . For samples drawn from a Gaussian distribution
the variance of
. For samples drawn from a Gaussian distribution
the variance of 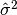 itself is
itself is 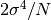 .
.This function computes the mean via a call to
gsl_stats_mean(). If you have already computed the mean then you can pass it directly togsl_stats_variance_m().
-
double gsl_stats_variance_m(const double data[], size_t stride, size_t n, double mean)¶
This function returns the sample variance of
datarelative to the given value ofmean. The function is computed with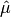 replaced by the value of
replaced by the value of meanthat you supply,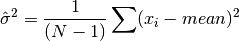
-
double gsl_stats_sd(const double data[], size_t stride, size_t n)¶
-
double gsl_stats_sd_m(const double data[], size_t stride, size_t n, double mean)¶
The standard deviation is defined as the square root of the variance. These functions return the square root of the corresponding variance functions above.
-
double gsl_stats_tss(const double data[], size_t stride, size_t n)¶
-
double gsl_stats_tss_m(const double data[], size_t stride, size_t n, double mean)¶
These functions return the total sum of squares (TSS) of
dataabout the mean. Forgsl_stats_tss_m()the user-supplied value ofmeanis used, and forgsl_stats_tss()it is computed usinggsl_stats_mean().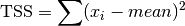
-
double gsl_stats_variance_with_fixed_mean(const double data[], size_t stride, size_t n, double mean)¶
This function computes an unbiased estimate of the variance of
datawhen the population meanmeanof the underlying distribution is known a priori. In this case the estimator for the variance uses the factor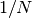 and the sample mean
and the sample mean
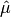 is replaced by the known population mean
is replaced by the known population mean 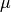 ,
,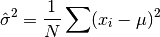
Absolute deviation¶
-
double gsl_stats_absdev(const double data[], size_t stride, size_t n)¶
This function computes the absolute deviation from the mean of
data, a dataset of lengthnwith stridestride. The absolute deviation from the mean is defined as,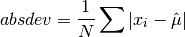
where
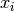 are the elements of the dataset
are the elements of the dataset data. The absolute deviation from the mean provides a more robust measure of the width of a distribution than the variance. This function computes the mean ofdatavia a call togsl_stats_mean().
-
double gsl_stats_absdev_m(const double data[], size_t stride, size_t n, double mean)¶
This function computes the absolute deviation of the dataset
datarelative to the given value ofmean,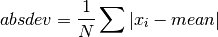
This function is useful if you have already computed the mean of
data(and want to avoid recomputing it), or wish to calculate the absolute deviation relative to another value (such as zero, or the median).
Higher moments (skewness and kurtosis)¶
-
double gsl_stats_skew(const double data[], size_t stride, size_t n)¶
This function computes the skewness of
data, a dataset of lengthnwith stridestride. The skewness is defined as,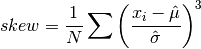
where
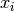 are the elements of the dataset
are the elements of the dataset data. The skewness measures the asymmetry of the tails of a distribution.The function computes the mean and estimated standard deviation of
datavia calls togsl_stats_mean()andgsl_stats_sd().
-
double gsl_stats_skew_m_sd(const double data[], size_t stride, size_t n, double mean, double sd)¶
This function computes the skewness of the dataset
datausing the given values of the meanmeanand standard deviationsd,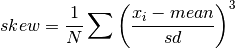
These functions are useful if you have already computed the mean and standard deviation of
dataand want to avoid recomputing them.
-
double gsl_stats_kurtosis(const double data[], size_t stride, size_t n)¶
This function computes the kurtosis of
data, a dataset of lengthnwith stridestride. The kurtosis is defined as,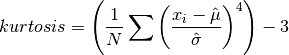
The kurtosis measures how sharply peaked a distribution is, relative to its width. The kurtosis is normalized to zero for a Gaussian distribution.
-
double gsl_stats_kurtosis_m_sd(const double data[], size_t stride, size_t n, double mean, double sd)¶
This function computes the kurtosis of the dataset
datausing the given values of the meanmeanand standard deviationsd,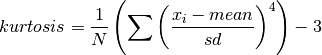
This function is useful if you have already computed the mean and standard deviation of
dataand want to avoid recomputing them.
Autocorrelation¶
Covariance¶
-
double gsl_stats_covariance(const double data1[], const size_t stride1, const double data2[], const size_t stride2, const size_t n)¶
This function computes the covariance of the datasets
data1anddata2which must both be of the same lengthn.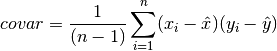
-
double gsl_stats_covariance_m(const double data1[], const size_t stride1, const double data2[], const size_t stride2, const size_t n, const double mean1, const double mean2)¶
This function computes the covariance of the datasets
data1anddata2using the given values of the means,mean1andmean2. This is useful if you have already computed the means ofdata1anddata2and want to avoid recomputing them.
Correlation¶
-
double gsl_stats_correlation(const double data1[], const size_t stride1, const double data2[], const size_t stride2, const size_t n)¶
This function efficiently computes the Pearson correlation coefficient between the datasets
data1anddata2which must both be of the same lengthn.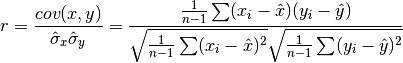
-
double gsl_stats_spearman(const double data1[], const size_t stride1, const double data2[], const size_t stride2, const size_t n, double work[])¶
This function computes the Spearman rank correlation coefficient between the datasets
data1anddata2which must both be of the same lengthn. Additional workspace of size 2 *nis required inwork. The Spearman rank correlation between vectors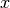 and
and
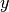 is equivalent to the Pearson correlation between the ranked
vectors
is equivalent to the Pearson correlation between the ranked
vectors 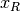 and
and 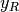 , where ranks are defined to be the
average of the positions of an element in the ascending order of the values.
, where ranks are defined to be the
average of the positions of an element in the ascending order of the values.
Weighted Samples¶
The functions described in this section allow the computation of
statistics for weighted samples. The functions accept an array of
samples, 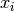 , with associated weights,
, with associated weights, 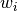 . Each sample
. Each sample
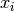 is considered as having been drawn from a Gaussian
distribution with variance
is considered as having been drawn from a Gaussian
distribution with variance 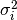 . The sample weight
. The sample weight
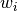 is defined as the reciprocal of this variance,
is defined as the reciprocal of this variance, 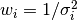 .
Setting a weight to zero corresponds to removing a sample from a dataset.
.
Setting a weight to zero corresponds to removing a sample from a dataset.
-
double gsl_stats_wmean(const double w[], size_t wstride, const double data[], size_t stride, size_t n)¶
This function returns the weighted mean of the dataset
datawith stridestrideand lengthn, using the set of weightswwith stridewstrideand lengthn. The weighted mean is defined as,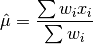
-
double gsl_stats_wvariance(const double w[], size_t wstride, const double data[], size_t stride, size_t n)¶
This function returns the estimated variance of the dataset
datawith stridestrideand lengthn, using the set of weightswwith stridewstrideand lengthn. The estimated variance of a weighted dataset is calculated as,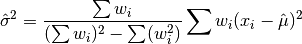
Note that this expression reduces to an unweighted variance with the familiar
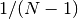 factor when there are
factor when there are 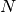 equal non-zero
weights.
equal non-zero
weights.
-
double gsl_stats_wvariance_m(const double w[], size_t wstride, const double data[], size_t stride, size_t n, double wmean)¶
This function returns the estimated variance of the weighted dataset
datausing the given weighted meanwmean.
-
double gsl_stats_wsd(const double w[], size_t wstride, const double data[], size_t stride, size_t n)¶
The standard deviation is defined as the square root of the variance. This function returns the square root of the corresponding variance function
gsl_stats_wvariance()above.
-
double gsl_stats_wsd_m(const double w[], size_t wstride, const double data[], size_t stride, size_t n, double wmean)¶
This function returns the square root of the corresponding variance function
gsl_stats_wvariance_m()above.
-
double gsl_stats_wvariance_with_fixed_mean(const double w[], size_t wstride, const double data[], size_t stride, size_t n, const double mean)¶
This function computes an unbiased estimate of the variance of the weighted dataset
datawhen the population meanmeanof the underlying distribution is known a priori. In this case the estimator for the variance replaces the sample mean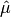 by the known
population mean
by the known
population mean 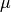 ,
,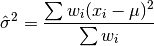
-
double gsl_stats_wsd_with_fixed_mean(const double w[], size_t wstride, const double data[], size_t stride, size_t n, const double mean)¶
The standard deviation is defined as the square root of the variance. This function returns the square root of the corresponding variance function above.
-
double gsl_stats_wtss(const double w[], const size_t wstride, const double data[], size_t stride, size_t n)¶
-
double gsl_stats_wtss_m(const double w[], const size_t wstride, const double data[], size_t stride, size_t n, double wmean)¶
These functions return the weighted total sum of squares (TSS) of
dataabout the weighted mean. Forgsl_stats_wtss_m()the user-supplied value ofwmeanis used, and forgsl_stats_wtss()it is computed usinggsl_stats_wmean().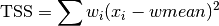
-
double gsl_stats_wabsdev(const double w[], size_t wstride, const double data[], size_t stride, size_t n)¶
This function computes the weighted absolute deviation from the weighted mean of
data. The absolute deviation from the mean is defined as,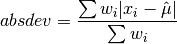
-
double gsl_stats_wabsdev_m(const double w[], size_t wstride, const double data[], size_t stride, size_t n, double wmean)¶
This function computes the absolute deviation of the weighted dataset
dataabout the given weighted meanwmean.
-
double gsl_stats_wskew(const double w[], size_t wstride, const double data[], size_t stride, size_t n)¶
This function computes the weighted skewness of the dataset
data.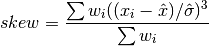
-
double gsl_stats_wskew_m_sd(const double w[], size_t wstride, const double data[], size_t stride, size_t n, double wmean, double wsd)¶
This function computes the weighted skewness of the dataset
datausing the given values of the weighted mean and weighted standard deviation,wmeanandwsd.
Maximum and Minimum values¶
The following functions find the maximum and minimum values of a
dataset (or their indices). If the data contains NaN-s then a
NaN will be returned, since the maximum or minimum value is
undefined. For functions which return an index, the location of the
first NaN in the array is returned.
-
double gsl_stats_max(const double data[], size_t stride, size_t n)¶
This function returns the maximum value in
data, a dataset of lengthnwith stridestride. The maximum value is defined as the value of the element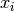 which satisfies
which satisfies 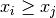 for all
for all 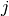 .
.If you want instead to find the element with the largest absolute magnitude you will need to apply
fabs()orabs()to your data before calling this function.
-
double gsl_stats_min(const double data[], size_t stride, size_t n)¶
This function returns the minimum value in
data, a dataset of lengthnwith stridestride. The minimum value is defined as the value of the element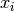 which satisfies
which satisfies 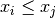 for all
for all 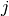 .
.If you want instead to find the element with the smallest absolute magnitude you will need to apply
fabs()orabs()to your data before calling this function.
-
void gsl_stats_minmax(double *min, double *max, const double data[], size_t stride, size_t n)¶
This function finds both the minimum and maximum values
min,maxindatain a single pass.
-
size_t gsl_stats_max_index(const double data[], size_t stride, size_t n)¶
This function returns the index of the maximum value in
data, a dataset of lengthnwith stridestride. The maximum value is defined as the value of the element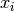 which satisfies
which satisfies
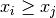 for all
for all 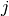 . When there are several equal maximum
elements then the first one is chosen.
. When there are several equal maximum
elements then the first one is chosen.
-
size_t gsl_stats_min_index(const double data[], size_t stride, size_t n)¶
This function returns the index of the minimum value in
data, a dataset of lengthnwith stridestride. The minimum value is defined as the value of the element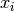 which satisfies
which satisfies
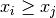 for all
for all 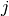 . When there are several equal
minimum elements then the first one is chosen.
. When there are several equal
minimum elements then the first one is chosen.
Median and Percentiles¶
The median and percentile functions described in this section operate on
sorted data in 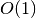 time. There is also a routine for computing
the median of an unsorted input array in average
time. There is also a routine for computing
the median of an unsorted input array in average 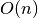 time using
the quickselect algorithm. For convenience we use quantiles, measured on a scale
of 0 to 1, instead of percentiles (which use a scale of 0 to 100).
time using
the quickselect algorithm. For convenience we use quantiles, measured on a scale
of 0 to 1, instead of percentiles (which use a scale of 0 to 100).
-
double gsl_stats_median_from_sorted_data(const double sorted_data[], const size_t stride, const size_t n)¶
This function returns the median value of
sorted_data, a dataset of lengthnwith stridestride. The elements of the array must be in ascending numerical order. There are no checks to see whether the data are sorted, so the functiongsl_sort()should always be used first.When the dataset has an odd number of elements the median is the value of element
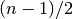 . When the dataset has an even number of
elements the median is the mean of the two nearest middle values,
elements
. When the dataset has an even number of
elements the median is the mean of the two nearest middle values,
elements 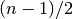 and
and 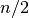 . Since the algorithm for
computing the median involves interpolation this function always returns
a floating-point number, even for integer data types.
. Since the algorithm for
computing the median involves interpolation this function always returns
a floating-point number, even for integer data types.
-
double gsl_stats_median(double data[], const size_t stride, const size_t n)¶
This function returns the median value of
data, a dataset of lengthnwith stridestride. The median is found using the quickselect algorithm. The input array does not need to be sorted, but note that the algorithm rearranges the array and so the input is not preserved on output.
-
double gsl_stats_quantile_from_sorted_data(const double sorted_data[], size_t stride, size_t n, double f)¶
This function returns a quantile value of
sorted_data, a double-precision array of lengthnwith stridestride. The elements of the array must be in ascending numerical order. The quantile is determined by thef, a fraction between 0 and 1. For example, to compute the value of the 75th percentilefshould have the value 0.75.There are no checks to see whether the data are sorted, so the function
gsl_sort()should always be used first.The quantile is found by interpolation, using the formula
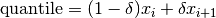
where
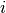 is
is floor((n - 1)f)and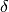 is
is
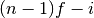 .
.Thus the minimum value of the array (
data[0*stride]) is given byfequal to zero, the maximum value (data[(n-1)*stride]) is given byfequal to one and the median value is given byfequal to 0.5. Since the algorithm for computing quantiles involves interpolation this function always returns a floating-point number, even for integer data types.
Order Statistics¶
The 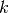 -th order statistic of a sample is equal to its
-th order statistic of a sample is equal to its 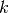 -th smallest value.
The
-th smallest value.
The 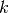 -th order statistic of a set of
-th order statistic of a set of 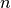 values
values 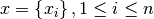 is
denoted
is
denoted 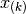 . The median of the set
. The median of the set 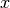 is equal to
is equal to 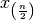 if
if
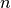 is odd, or the average of
is odd, or the average of 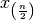 and
and 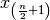 if
if 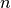 is even. The
is even. The 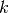 -th smallest element of a length
-th smallest element of a length 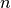 vector can be found
in average
vector can be found
in average 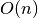 time using the quickselect algorithm.
time using the quickselect algorithm.
-
double gsl_stats_select(double data[], const size_t stride, const size_t n, const size_t k)¶
This function finds the
k-th smallest element of the input arraydataof lengthnand stridestrideusing the quickselect method. The algorithm rearranges the elements ofdataand so the input array is not preserved on output.
Robust Location Estimates¶
A location estimate refers to a typical or central value which best describes a given dataset. The mean and median are both examples of location estimators. However, the mean has a severe sensitivity to data outliers and can give erroneous values when even a small number of outliers are present. The median on the other hand, has a strong insensitivity to data outliers, but due to its non-smoothness it can behave unexpectedly in certain situations. GSL offers the following alternative location estimators, which are robust to the presence of outliers.
Trimmed Mean¶
The trimmed mean, or truncated mean, discards a certain number of smallest and largest
samples from the input vector before computing the mean of the remaining samples. The
amount of trimming is specified by a factor ![\alpha \in [0,0.5]](_images/math/fd05efebd98c2398ee308a6f3d97af8ba1390345.png) . Then the
number of samples discarded from both ends of the input vector is
. Then the
number of samples discarded from both ends of the input vector is
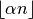 , where
, where 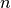 is the length of the input.
So to discard 25% of the samples from each end, one would set
is the length of the input.
So to discard 25% of the samples from each end, one would set 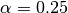 .
.
-
double gsl_stats_trmean_from_sorted_data(const double alpha, const double sorted_data[], const size_t stride, const size_t n)¶
This function returns the trimmed mean of
sorted_data, a dataset of lengthnwith stridestride. The elements of the array must be in ascending numerical order. There are no checks to see whether the data are sorted, so the functiongsl_sort()should always be used first. The trimming factor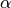 is given in
is given in alpha. If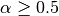 , then the median of the input is returned.
, then the median of the input is returned.
Gastwirth Estimator¶
Gastwirth’s location estimator is a weighted sum of three order statistics,
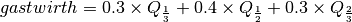
where 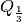 is the one-third quantile,
is the one-third quantile, 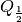 is the one-half
quantile (i.e. median), and
is the one-half
quantile (i.e. median), and  is the two-thirds quantile.
is the two-thirds quantile.
-
double gsl_stats_gastwirth_from_sorted_data(const double sorted_data[], const size_t stride, const size_t n)¶
This function returns the Gastwirth location estimator of
sorted_data, a dataset of lengthnwith stridestride. The elements of the array must be in ascending numerical order. There are no checks to see whether the data are sorted, so the functiongsl_sort()should always be used first.
Robust Scale Estimates¶
A robust scale estimate, also known as a robust measure of scale, attempts to quantify the statistical dispersion (variability, scatter, spread) in a set of data which may contain outliers. In such datasets, the usual variance or standard deviation scale estimate can be rendered useless by even a single outlier.
Median Absolute Deviation (MAD)¶
The median absolute deviation (MAD) is defined as
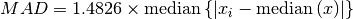
In words, first the median of all samples is computed. Then the median
is subtracted from all samples in the input to find the deviation of each sample
from the median. The median of all absolute deviations is then the MAD.
The factor 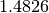 makes the MAD an unbiased estimator of the standard deviation for Gaussian data.
The median absolute deviation has an asymptotic efficiency of 37%.
makes the MAD an unbiased estimator of the standard deviation for Gaussian data.
The median absolute deviation has an asymptotic efficiency of 37%.
-
double gsl_stats_mad0(const double data[], const size_t stride, const size_t n, double work[])¶
-
double gsl_stats_mad(const double data[], const size_t stride, const size_t n, double work[])¶
These functions return the median absolute deviation of
data, a dataset of lengthnand stridestride. Themad0function calculates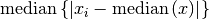 (i.e. the
(i.e. the 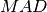 statistic without the bias correction scale factor).
These functions require additional workspace of size
statistic without the bias correction scale factor).
These functions require additional workspace of size nprovided inwork.
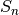 Statistic¶
Statistic¶
The 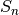 statistic developed by Croux and Rousseeuw is defined as
statistic developed by Croux and Rousseeuw is defined as
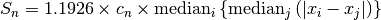
For each sample 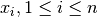 , the median of the values
, the median of the values 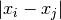 is computed for all
is computed for all
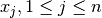 . This yields
. This yields 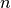 values, whose median then gives the final
values, whose median then gives the final 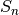 .
The factor
.
The factor 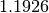 makes
makes 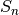 an unbiased estimate of the standard deviation for Gaussian data.
The factor
an unbiased estimate of the standard deviation for Gaussian data.
The factor 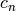 is a correction factor to correct bias in small sample sizes.
is a correction factor to correct bias in small sample sizes. 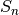 has an asymptotic
efficiency of 58%.
has an asymptotic
efficiency of 58%.
-
double gsl_stats_Sn0_from_sorted_data(const double sorted_data[], const size_t stride, const size_t n, double work[])¶
-
double gsl_stats_Sn_from_sorted_data(const double sorted_data[], const size_t stride, const size_t n, double work[])¶
These functions return the
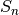 statistic of
statistic of sorted_data, a dataset of lengthnwith stridestride. The elements of the array must be in ascending numerical order. There are no checks to see whether the data are sorted, so the functiongsl_sort()should always be used first. TheSn0function calculates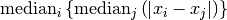 (i.e. the
(i.e. the 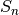 statistic without the bias correction scale factors).
These functions require additional workspace of size
statistic without the bias correction scale factors).
These functions require additional workspace of size
nprovided inwork.
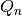 Statistic¶
Statistic¶
The 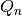 statistic developed by Croux and Rousseeuw is defined as
statistic developed by Croux and Rousseeuw is defined as
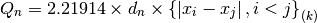
The factor  makes
makes 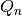 an unbiased estimate of the standard deviation for Gaussian data.
The factor
an unbiased estimate of the standard deviation for Gaussian data.
The factor 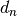 is a correction factor to correct bias in small sample sizes. The order statistic
is
is a correction factor to correct bias in small sample sizes. The order statistic
is
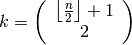
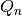 has an asymptotic efficiency of 82%.
has an asymptotic efficiency of 82%.
-
double gsl_stats_Qn0_from_sorted_data(const double sorted_data[], const size_t stride, const size_t n, double work[], int work_int[])¶
-
double gsl_stats_Qn_from_sorted_data(const double sorted_data[], const size_t stride, const size_t n, double work[], int work_int[])¶
These functions return the
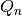 statistic of
statistic of sorted_data, a dataset of lengthnwith stridestride. The elements of the array must be in ascending numerical order. There are no checks to see whether the data are sorted, so the functiongsl_sort()should always be used first. TheQn0function calculates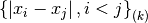 (i.e.
(i.e. 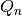 without the bias correction scale factors).
These functions require additional workspace of size
without the bias correction scale factors).
These functions require additional workspace of size
3nprovided inworkand integer workspace of size5nprovided inwork_int.
Examples¶
Here is a basic example of how to use the statistical functions:
#include <stdio.h>
#include <gsl/gsl_statistics.h>
int
main(void)
{
double data[5] = {17.2, 18.1, 16.5, 18.3, 12.6};
double mean, variance, largest, smallest;
mean = gsl_stats_mean(data, 1, 5);
variance = gsl_stats_variance(data, 1, 5);
largest = gsl_stats_max(data, 1, 5);
smallest = gsl_stats_min(data, 1, 5);
printf ("The dataset is %g, %g, %g, %g, %g\n",
data[0], data[1], data[2], data[3], data[4]);
printf ("The sample mean is %g\n", mean);
printf ("The estimated variance is %g\n", variance);
printf ("The largest value is %g\n", largest);
printf ("The smallest value is %g\n", smallest);
return 0;
}
The program should produce the following output,
The dataset is 17.2, 18.1, 16.5, 18.3, 12.6
The sample mean is 16.54
The estimated variance is 5.373
The largest value is 18.3
The smallest value is 12.6
Here is an example using sorted data,
#include <stdio.h>
#include <gsl/gsl_sort.h>
#include <gsl/gsl_statistics.h>
int
main(void)
{
double data[5] = {17.2, 18.1, 16.5, 18.3, 12.6};
double median, upperq, lowerq;
printf ("Original dataset: %g, %g, %g, %g, %g\n",
data[0], data[1], data[2], data[3], data[4]);
gsl_sort (data, 1, 5);
printf ("Sorted dataset: %g, %g, %g, %g, %g\n",
data[0], data[1], data[2], data[3], data[4]);
median
= gsl_stats_median_from_sorted_data (data,
1, 5);
upperq
= gsl_stats_quantile_from_sorted_data (data,
1, 5,
0.75);
lowerq
= gsl_stats_quantile_from_sorted_data (data,
1, 5,
0.25);
printf ("The median is %g\n", median);
printf ("The upper quartile is %g\n", upperq);
printf ("The lower quartile is %g\n", lowerq);
return 0;
}
This program should produce the following output,
Original dataset: 17.2, 18.1, 16.5, 18.3, 12.6
Sorted dataset: 12.6, 16.5, 17.2, 18.1, 18.3
The median is 17.2
The upper quartile is 18.1
The lower quartile is 16.5
References and Further Reading¶
The standard reference for almost any topic in statistics is the multi-volume Advanced Theory of Statistics by Kendall and Stuart.
Maurice Kendall, Alan Stuart, and J. Keith Ord. The Advanced Theory of Statistics (multiple volumes) reprinted as Kendall’s Advanced Theory of Statistics. Wiley, ISBN 047023380X.
Many statistical concepts can be more easily understood by a Bayesian approach. The following book by Gelman, Carlin, Stern and Rubin gives a comprehensive coverage of the subject.
Andrew Gelman, John B. Carlin, Hal S. Stern, Donald B. Rubin. Bayesian Data Analysis. Chapman & Hall, ISBN 0412039915.
For physicists the Particle Data Group provides useful reviews of Probability and Statistics in the “Mathematical Tools” section of its Annual Review of Particle Physics.
Review of Particle Properties, R.M. Barnett et al., Physical Review D54, 1 (1996)
The Review of Particle Physics is available online at the website http://pdg.lbl.gov/.
The following papers describe robust scale estimation,
C. Croux and P. J. Rousseeuw, Time-Efficient algorithms for two highly robust estimators of scale, Comp. Stat., Physica, Heidelberg, 1992.
P. J. Rousseeuw and C. Croux, Explicit scale estimators with high breakdown point, L1-Statistical Analysis and Related Methods, pp. 77-92, 1992.