Wavelet Transforms¶
This chapter describes functions for performing Discrete Wavelet
Transforms (DWTs). The library includes wavelets for real data in both
one and two dimensions. The wavelet functions are declared in the header
files gsl_wavelet.h and gsl_wavelet2d.h.
Definitions¶
The continuous wavelet transform and its inverse are defined by the relations,
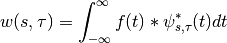
and,
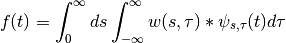
where the basis functions 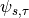 are obtained by scaling
and translation from a single function, referred to as the mother wavelet.
are obtained by scaling
and translation from a single function, referred to as the mother wavelet.
The discrete version of the wavelet transform acts on equally-spaced
samples, with fixed scaling and translation steps ( ,
,
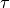 ). The frequency and time axes are sampled dyadically
on scales of
). The frequency and time axes are sampled dyadically
on scales of 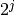 through a level parameter
through a level parameter 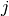 .
.
The resulting family of functions 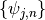 constitutes an orthonormal basis for square-integrable signals.
The discrete wavelet transform is an
constitutes an orthonormal basis for square-integrable signals.
The discrete wavelet transform is an 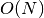 algorithm, and is also
referred to as the fast wavelet transform.
algorithm, and is also
referred to as the fast wavelet transform.
Initialization¶
-
type gsl_wavelet¶
This structure contains the filter coefficients defining the wavelet and any associated offset parameters.
-
gsl_wavelet *gsl_wavelet_alloc(const gsl_wavelet_type *T, size_t k)¶
This function allocates and initializes a wavelet object of type
T. The parameterkselects the specific member of the wavelet family. A null pointer is returned if insufficient memory is available or if a unsupported member is selected.
The following wavelet types are implemented:
-
type gsl_wavelet_type¶
-
gsl_wavelet_type *gsl_wavelet_daubechies¶
-
gsl_wavelet_type *gsl_wavelet_daubechies_centered¶
This is the Daubechies wavelet family of maximum phase with
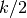 vanishing moments. The implemented wavelets are
vanishing moments. The implemented wavelets are
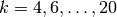 , with
, with keven.
-
gsl_wavelet_type *gsl_wavelet_haar¶
-
gsl_wavelet_type *gsl_wavelet_haar_centered¶
This is the Haar wavelet. The only valid choice of
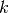 for the
Haar wavelet is
for the
Haar wavelet is 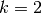 .
.
-
gsl_wavelet_type *gsl_wavelet_bspline¶
-
gsl_wavelet_type *gsl_wavelet_bspline_centered¶
This is the biorthogonal B-spline wavelet family of order
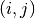 .
The implemented values of
.
The implemented values of 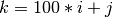 are 103, 105, 202, 204,
206, 208, 301, 303, 305 307, 309.
are 103, 105, 202, 204,
206, 208, 301, 303, 305 307, 309.
-
gsl_wavelet_type *gsl_wavelet_daubechies¶
The centered forms of the wavelets align the coefficients of the various sub-bands on edges. Thus the resulting visualization of the coefficients of the wavelet transform in the phase plane is easier to understand.
-
const char *gsl_wavelet_name(const gsl_wavelet *w)¶
This function returns a pointer to the name of the wavelet family for
w.
-
void gsl_wavelet_free(gsl_wavelet *w)¶
This function frees the wavelet object
w.
-
type gsl_wavelet_workspace¶
This structure contains scratch space of the same size as the input data and is used to hold intermediate results during the transform.
-
gsl_wavelet_workspace *gsl_wavelet_workspace_alloc(size_t n)¶
This function allocates a workspace for the discrete wavelet transform. To perform a one-dimensional transform on
nelements, a workspace of sizenmust be provided. For two-dimensional transforms ofn-by-nmatrices it is sufficient to allocate a workspace of sizen, since the transform operates on individual rows and columns. A null pointer is returned if insufficient memory is available.
-
void gsl_wavelet_workspace_free(gsl_wavelet_workspace *work)¶
This function frees the allocated workspace
work.
Transform Functions¶
This sections describes the actual functions performing the discrete wavelet transform. Note that the transforms use periodic boundary conditions. If the signal is not periodic in the sample length then spurious coefficients will appear at the beginning and end of each level of the transform.
Wavelet transforms in one dimension¶
-
int gsl_wavelet_transform(const gsl_wavelet *w, double *data, size_t stride, size_t n, gsl_wavelet_direction dir, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet_transform_forward(const gsl_wavelet *w, double *data, size_t stride, size_t n, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet_transform_inverse(const gsl_wavelet *w, double *data, size_t stride, size_t n, gsl_wavelet_workspace *work)¶
These functions compute in-place forward and inverse discrete wavelet transforms of length
nwith stridestrideon the arraydata. The length of the transformnis restricted to powers of two. For thetransformversion of the function the argumentdircan be eitherforward(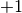 ) or
) or backward(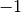 ). A workspace
). A workspace workof lengthnmust be provided.For the forward transform, the elements of the original array are replaced by the discrete wavelet transform
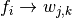 in a packed triangular storage layout,
where
in a packed triangular storage layout,
where jis the index of the level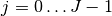 and
and
kis the index of the coefficient within each level, .
The total number of levels is
.
The total number of levels is 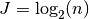 . The output data
has the following form,
. The output data
has the following form,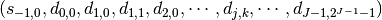
where the first element is the smoothing coefficient
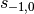 ,
followed by the detail coefficients
,
followed by the detail coefficients 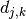 for each level
for each level
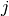 . The backward transform inverts these coefficients to obtain
the original data.
. The backward transform inverts these coefficients to obtain
the original data.These functions return a status of
GSL_SUCCESSupon successful completion.GSL_EINVALis returned ifnis not an integer power of 2 or if insufficient workspace is provided.
Wavelet transforms in two dimension¶
The library provides functions to perform two-dimensional discrete wavelet transforms on square matrices. The matrix dimensions must be an integer power of two. There are two possible orderings of the rows and columns in the two-dimensional wavelet transform, referred to as the “standard” and “non-standard” forms.
The “standard” transform performs a complete discrete wavelet transform on the rows of the matrix, followed by a separate complete discrete wavelet transform on the columns of the resulting row-transformed matrix. This procedure uses the same ordering as a two-dimensional Fourier transform.
The “non-standard” transform is performed in interleaved passes on the rows and columns of the matrix for each level of the transform. The first level of the transform is applied to the matrix rows, and then to the matrix columns. This procedure is then repeated across the rows and columns of the data for the subsequent levels of the transform, until the full discrete wavelet transform is complete. The non-standard form of the discrete wavelet transform is typically used in image analysis.
The functions described in this section are declared in the header file
gsl_wavelet2d.h.
-
int gsl_wavelet2d_transform(const gsl_wavelet *w, double *data, size_t tda, size_t size1, size_t size2, gsl_wavelet_direction dir, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet2d_transform_forward(const gsl_wavelet *w, double *data, size_t tda, size_t size1, size_t size2, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet2d_transform_inverse(const gsl_wavelet *w, double *data, size_t tda, size_t size1, size_t size2, gsl_wavelet_workspace *work)¶
These functions compute two-dimensional in-place forward and inverse discrete wavelet transforms in standard form on the array
datastored in row-major form with dimensionssize1andsize2and physical row lengthtda. The dimensions must be equal (square matrix) and are restricted to powers of two. For thetransformversion of the function the argumentdircan be eitherforward(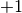 ) or
) or backward( ). A
workspace
). A
workspace workof the appropriate size must be provided. On exit, the appropriate elements of the arraydataare replaced by their two-dimensional wavelet transform.The functions return a status of
GSL_SUCCESSupon successful completion.GSL_EINVALis returned ifsize1andsize2are not equal and integer powers of 2, or if insufficient workspace is provided.
-
int gsl_wavelet2d_transform_matrix(const gsl_wavelet *w, gsl_matrix *m, gsl_wavelet_direction dir, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet2d_transform_matrix_forward(const gsl_wavelet *w, gsl_matrix *m, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet2d_transform_matrix_inverse(const gsl_wavelet *w, gsl_matrix *m, gsl_wavelet_workspace *work)¶
These functions compute the two-dimensional in-place wavelet transform on a matrix
m.
-
int gsl_wavelet2d_nstransform(const gsl_wavelet *w, double *data, size_t tda, size_t size1, size_t size2, gsl_wavelet_direction dir, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet2d_nstransform_forward(const gsl_wavelet *w, double *data, size_t tda, size_t size1, size_t size2, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet2d_nstransform_inverse(const gsl_wavelet *w, double *data, size_t tda, size_t size1, size_t size2, gsl_wavelet_workspace *work)¶
These functions compute the two-dimensional wavelet transform in non-standard form.
-
int gsl_wavelet2d_nstransform_matrix(const gsl_wavelet *w, gsl_matrix *m, gsl_wavelet_direction dir, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet2d_nstransform_matrix_forward(const gsl_wavelet *w, gsl_matrix *m, gsl_wavelet_workspace *work)¶
-
int gsl_wavelet2d_nstransform_matrix_inverse(const gsl_wavelet *w, gsl_matrix *m, gsl_wavelet_workspace *work)¶
These functions compute the non-standard form of the two-dimensional in-place wavelet transform on a matrix
m.
Examples¶
The following program demonstrates the use of the one-dimensional wavelet transform functions. It computes an approximation to an input signal (of length 256) using the 20 largest components of the wavelet transform, while setting the others to zero.
#include <stdio.h>
#include <math.h>
#include <gsl/gsl_sort.h>
#include <gsl/gsl_wavelet.h>
int
main (int argc, char **argv)
{
(void)(argc); /* avoid unused parameter warning */
int i, n = 256, nc = 20;
double *orig_data = malloc (n * sizeof (double));
double *data = malloc (n * sizeof (double));
double *abscoeff = malloc (n * sizeof (double));
size_t *p = malloc (n * sizeof (size_t));
FILE * f;
gsl_wavelet *w;
gsl_wavelet_workspace *work;
w = gsl_wavelet_alloc (gsl_wavelet_daubechies, 4);
work = gsl_wavelet_workspace_alloc (n);
f = fopen (argv[1], "r");
for (i = 0; i < n; i++)
{
fscanf (f, "%lg", &orig_data[i]);
data[i] = orig_data[i];
}
fclose (f);
gsl_wavelet_transform_forward (w, data, 1, n, work);
for (i = 0; i < n; i++)
{
abscoeff[i] = fabs (data[i]);
}
gsl_sort_index (p, abscoeff, 1, n);
for (i = 0; (i + nc) < n; i++)
data[p[i]] = 0;
gsl_wavelet_transform_inverse (w, data, 1, n, work);
for (i = 0; i < n; i++)
{
printf ("%g %g\n", orig_data[i], data[i]);
}
gsl_wavelet_free (w);
gsl_wavelet_workspace_free (work);
free (data);
free (orig_data);
free (abscoeff);
free (p);
return 0;
}
The output can be used with the GNU plotutils graph program:
$ ./a.out ecg.dat > dwt.txt
$ graph -T ps -x 0 256 32 -h 0.3 -a dwt.txt > dwt.ps
Fig. 27 shows an original and compressed version of a sample ECG recording from the MIT-BIH Arrhythmia Database, part of the PhysioNet archive of public-domain of medical datasets.
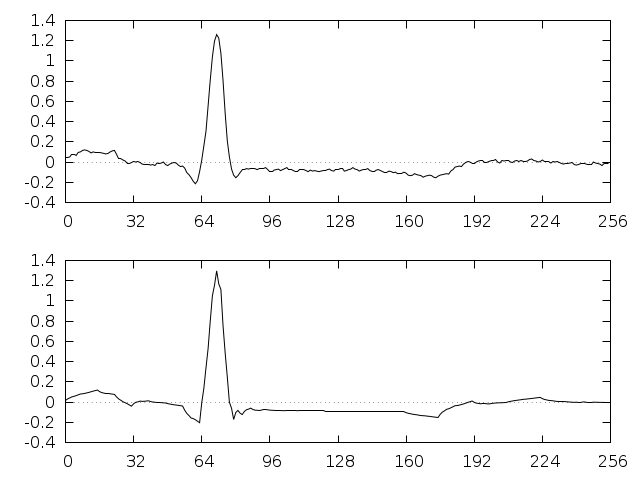
Fig. 27 Original (upper) and wavelet-compressed (lower) ECG signals, using the 20 largest components of the Daubechies(4) discrete wavelet transform.¶
References and Further Reading¶
The mathematical background to wavelet transforms is covered in the original lectures by Daubechies,
Ingrid Daubechies. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics (1992), SIAM, ISBN 0898712742.
An easy to read introduction to the subject with an emphasis on the application of the wavelet transform in various branches of science is,
Paul S. Addison. The Illustrated Wavelet Transform Handbook. Institute of Physics Publishing (2002), ISBN 0750306920.
For extensive coverage of signal analysis by wavelets, wavelet packets and local cosine bases see,
S. G. Mallat. A wavelet tour of signal processing (Second edition). Academic Press (1999), ISBN 012466606X.
The concept of multiresolution analysis underlying the wavelet transform is described in,
S. G. Mallat. Multiresolution Approximations and Wavelet Orthonormal Bases of L^2(R). Transactions of the American Mathematical Society, 315(1), 1989, 69–87.
S. G. Mallat. A Theory for Multiresolution Signal Decomposition—The Wavelet Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11, 1989, 674–693.
The coefficients for the individual wavelet families implemented by the library can be found in the following papers,
I. Daubechies. Orthonormal Bases of Compactly Supported Wavelets. Communications on Pure and Applied Mathematics, 41 (1988) 909–996.
A. Cohen, I. Daubechies, and J.-C. Feauveau. Biorthogonal Bases of Compactly Supported Wavelets. Communications on Pure and Applied Mathematics, 45 (1992) 485–560.
The PhysioNet archive of physiological datasets can be found online at http://www.physionet.org/ and is described in the following paper,
Goldberger et al. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 101(23):e215-e220 2000.